
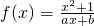 是奇函数且f(1)=2.(1)求a,b的值;(2)用定义判断f(x)在(-∞,-1)上的单调性.
是奇函数且f(1)=2.(1)求a,b的值;(2)用定义判断f(x)在(-∞,-1)上的单调性.
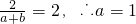
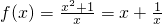
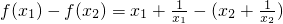 =
=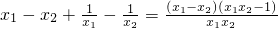 ,因为x1<x2<-1,所以x1-x2<0,x1x2>1,x1x2-1>0,所以f(x1)-f(x2)<0,f(x1)<f(x2)
,因为x1<x2<-1,所以x1-x2<0,x1x2>1,x1x2-1>0,所以f(x1)-f(x2)<0,f(x1)<f(x2)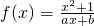 是奇函数得f(-x)=-f(x)即
是奇函数得f(-x)=-f(x)即 恒成立,化简得b=0,再由f(1)=2,可求得a值.
恒成立,化简得b=0,再由f(1)=2,可求得a值.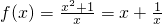 ,设x1,x2是(-∞,-1)上的任意两实数,且x1<x2,作差f(x1)-f(x2),将差化简为几个因子的乘积,再判断差的符号,用定义判断出结论.注意用定义法证明时的步骤.
,设x1,x2是(-∞,-1)上的任意两实数,且x1<x2,作差f(x1)-f(x2),将差化简为几个因子的乘积,再判断差的符号,用定义判断出结论.注意用定义法证明时的步骤.

科目:高中数学 来源: 题型:解答题
 是奇函数,函数f(x)的图象在点(1,f(1))处切线的斜率为-6,且当x=2时,函数f(x)有极值.
是奇函数,函数f(x)的图象在点(1,f(1))处切线的斜率为-6,且当x=2时,函数f(x)有极值.查看答案和解析>>
科目:高中数学 来源:2009-2010学年重庆市西南师大附中高三(上)9月月考数学试卷(文科)(解析版) 题型:解答题
 是奇函数,函数f(x)的图象在点(1,f(1))处切线的斜率为-6,且当x=2时,函数f(x)有极值.
是奇函数,函数f(x)的图象在点(1,f(1))处切线的斜率为-6,且当x=2时,函数f(x)有极值.查看答案和解析>>
科目:高中数学 来源:2010-2011学年云南省曲靖市陆良联中高一(上)数学周末练习(8)(解析版) 题型:解答题
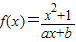 是奇函数且f(1)=2.(1)求a,b的值;(2)用定义判断f(x)在(-∞,-1)上的单调性.
是奇函数且f(1)=2.(1)求a,b的值;(2)用定义判断f(x)在(-∞,-1)上的单调性.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com