
【题目】如图,直三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点,△
的中点,△![]() 是等腰三角形,
是等腰三角形, ![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 上一点;
上一点;
(1)若![]() ∥平面
∥平面![]() ,求
,求![]() ;
;
(2)平面![]() 将三棱柱
将三棱柱![]() 分成两个部分,求含有点
分成两个部分,求含有点![]() 的那部分体积;
的那部分体积;

【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)因为![]() ∥平面
∥平面![]() ,所以找过直线DE的平面
,所以找过直线DE的平面![]() 与平面
与平面![]() 的交线,进而确定所求的值。取BC的中点N,连结MN,
的交线,进而确定所求的值。取BC的中点N,连结MN, ![]() ,根据
,根据![]() ∥
∥![]() ∥
∥![]() ,可得平面
,可得平面![]() 与平面
与平面![]() 为同一个平面,平面
为同一个平面,平面![]()
![]() 平面
平面![]()
![]() ,根据条件
,根据条件![]() ∥平面
∥平面![]() 和线面平行的性质定理可得
和线面平行的性质定理可得![]() ∥
∥![]() ,再由
,再由![]() 为
为![]() 的中点,可得
的中点,可得![]() 是
是![]() 的中点,∴
的中点,∴![]() .(2)含有点
.(2)含有点![]() 的那部分不是规则的几何体,体积不好求,故把该部分补成规则的几何体。延长MN至点F,使MN=NF,连结FC、FC1. 补成三棱柱
的那部分不是规则的几何体,体积不好求,故把该部分补成规则的几何体。延长MN至点F,使MN=NF,连结FC、FC1. 补成三棱柱![]() 所以所求部分的体积等于三棱柱
所以所求部分的体积等于三棱柱![]() 的体积减去三棱锥
的体积减去三棱锥![]() 的体积。因为三棱柱
的体积。因为三棱柱![]() 为直三棱柱,∴
为直三棱柱,∴![]() 平面
平面![]() ,
, ![]()
又因为![]() ,所以
,所以![]() 平面
平面![]() ,所以三棱柱
,所以三棱柱![]() 是直三棱柱。
是直三棱柱。
因为![]() 平面
平面![]() ,所以
,所以![]() ,所以三棱锥
,所以三棱锥![]() 为直三棱锥。∵
为直三棱锥。∵![]() ,又
,又![]() 是等腰三角形,所以
是等腰三角形,所以![]() . 因为BC的中点为N,所以
. 因为BC的中点为N,所以![]() .
.
试题解析:解:取![]() 中点为
中点为![]() ,连结
,连结![]() ,
,
 ∵
∵![]() 分别为
分别为![]() 中点
中点
∴![]() ∥
∥![]() ∥
∥![]() ,∴
,∴![]() 四点共面,
四点共面,
且平面![]()
![]() 平面
平面![]()
![]()
又![]() 平面
平面![]() ,且
,且![]() ∥平面
∥平面![]() ,∴
,∴![]() ∥
∥![]()
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() 是
是![]() 的中点,∴
的中点,∴![]() .
.
(2)因为三棱柱![]() 为直三棱柱,∴
为直三棱柱,∴![]() 平面
平面![]() ,
, ![]()
又![]() ,则
,则![]() 平面
平面![]() 。
。
∵![]() ,又
,又![]() 是等腰三角形,所以
是等腰三角形,所以![]() .
.
如图,将几何体![]() 补成三棱柱
补成三棱柱![]()
∴几何体![]() 的体积为:
的体积为: ![]()


科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足an+Sn=2.
(1)求数列{an}的通项公式;
(2)求证数列{an}中不存在三项按原来顺序成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某园林公司准备绿化一块半径为200米,圆心角为 ![]() 的扇形空地(如图的扇形OPQ区域),扇形的内接矩形ABCD为一水池,其余的地方种花,若∠COP=α,矩形ABCD的面积为S(单位:平方米).
的扇形空地(如图的扇形OPQ区域),扇形的内接矩形ABCD为一水池,其余的地方种花,若∠COP=α,矩形ABCD的面积为S(单位:平方米). 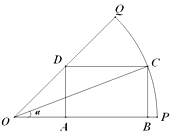
(1)试将S表示为关于α的函数,求出该函数的表达式;
(2)角α取何值时,水池的面积 S最大,并求出这个最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知常数![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,
, ![]() ,
, ![]() ;
;
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,且
,且![]() 是单调递增数列,求实数
是单调递增数列,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,
, ![]() ,对于任意给定的正整数
,对于任意给定的正整数![]() ,是否存在正整数
,是否存在正整数![]() 、
、![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 、
、![]() 的值(只要写出一组即可);若不存在,请说明理由;
的值(只要写出一组即可);若不存在,请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示:有三根针和套在一根针上的若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上.
(1)每次只能移动一个金属片;
(2)在每次移动过程中,每根针上较大的金属片不能放在较小的金属片上面.将n个金属片从1号针移到3号针最少需要移动的次数记为f(n);
①f(3)=;
②f(n)= . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2为椭圆 ![]() 的左、右焦点,F2在以
的左、右焦点,F2在以 ![]() 为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.
为圆心,1为半径的圆C2上,且|QF1|+|QF2|=2a.
(1)求椭圆C1的方程;
(2)过点P(0,1)的直线l1交椭圆C1于A,B两点,过P与l1垂直的直线l2交圆C2于C,D两点,M为线段CD中点,求△MAB面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,三角形ABC为等腰直角三角形,AC=BC= ![]() ,AA1=1,点D是AB的中点.
,AA1=1,点D是AB的中点. 
(1)求证:AC1∥平面CDB1;
(2)二面角B1﹣CD﹣B的平面角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com