
【题目】已知函数![]() .
.
(1)求函数![]() 的定义域;
的定义域;
(2)若函数![]() 的最小值为
的最小值为![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据对数函数的真数大于零列不等式组,解不等式组即可求得函数![]() 的定义域;(2)根据对数的运算法则化简函数的解析式,利用对数函数的单调性,结合二次函数的最值,求出函数的最小值,列出关于
的定义域;(2)根据对数的运算法则化简函数的解析式,利用对数函数的单调性,结合二次函数的最值,求出函数的最小值,列出关于![]() 的方程,解出即可.
的方程,解出即可.
试题解析:(1)要使函数有意义,则有![]() ,
,
解得![]() ,所以定义域为
,所以定义域为![]() .
.
(2)函数可化为![]()
![]()
![]()
![]() ,
, ![]()
![]()
又![]() ,
, ![]() ,即
,即![]() 的最小值为
的最小值为![]()
由![]() ,得
,得![]() ,
, ![]() .
.
【方法点晴】本题主要考查函数的定义域、二次函数的最值以及复合函数的单调性,属于中档题.定义域的三种类型及求法:(1)已知函数的解析式,则构造使解析式有意义的不等式(组)求解;(2) 对实际问题:由实际意义及使解析式有意义构成的不等式(组)求解;(3) 若已知函数![]() 的定义域为
的定义域为![]() ,则函数
,则函数![]() 的定义域由不等式
的定义域由不等式![]() 求出.
求出.


科目:高中数学 来源: 题型:
【题目】如图,已知双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左、右焦点分别为F1、F2 , |F1F2|=4,P是双曲线右支上一点,直线PF2交y轴于点A,△APF1的内切圆切边PF1于点Q,若|PQ|=1,则双曲线的离心率为 .
=1(a>0,b>0)的左、右焦点分别为F1、F2 , |F1F2|=4,P是双曲线右支上一点,直线PF2交y轴于点A,△APF1的内切圆切边PF1于点Q,若|PQ|=1,则双曲线的离心率为 . 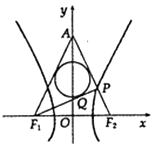
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() ,若f(a)=f(b)=f(c)=f(d),其中a,b,c,d互不相等,则对于命题p:abcd∈(0,1)和命题q:a+b+c+d∈[e+e﹣1﹣2,e2+e﹣2﹣2)真假的判断,正确的是( )
,若f(a)=f(b)=f(c)=f(d),其中a,b,c,d互不相等,则对于命题p:abcd∈(0,1)和命题q:a+b+c+d∈[e+e﹣1﹣2,e2+e﹣2﹣2)真假的判断,正确的是( )
A.p假q真
B.p假q假
C.p真q真
D.p真q假
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的首项a1=1,且(n+1)a ![]() +anan+1﹣na
+anan+1﹣na ![]() =0对n∈N*都成立.
=0对n∈N*都成立.
(1)求{an}的通项公式;
(2)记bn=a2n﹣1a2n+1 , 数列{bn}的前n项和为Tn , 证明:Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三条直线l1:4x+y-4=0,l2:mx+y=0,l3:2x-3my-4=0.
(1)若直线l1,l2,l3交于一点,求实数m的值;
(2)若直线l1,l2,l3不能围成三角形,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y=f(x)图象上不同两点A(x1 , y1),B(x2 , y2)处的切线的斜率分别是kA , kB , 规定φ(A,B)= ![]() (|AB|为线段AB的长度)叫做曲线y=f(x)在点A与点B之间的“弯曲度”,给出以下命题: ①函数y=x3图象上两点A与B的横坐标分别为1和﹣1,则φ(A,B)=0;
(|AB|为线段AB的长度)叫做曲线y=f(x)在点A与点B之间的“弯曲度”,给出以下命题: ①函数y=x3图象上两点A与B的横坐标分别为1和﹣1,则φ(A,B)=0;
②存在这样的函数,图象上任意两点之间的“弯曲度”为常数;
③设点A,B是抛物线y=x2+1上不同的两点,则φ(A,B)≤2;
④设曲线y=ex(e是自然对数的底数)上不同两点A(x1 , y1),B(x2 , y2),则φ(A,B)<1.
其中真命题的序号为 . (将所有真命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某经销商从沿海城市水产养殖厂购进一批某海鱼,随机抽取50条作为样本进行统计,按海鱼重量(克)得到如图的频率分布直方图: 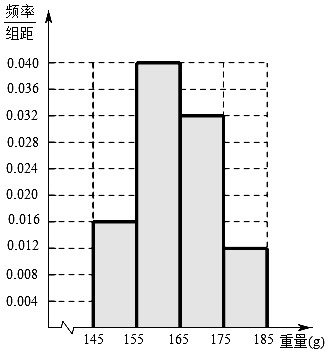
(Ⅰ)若经销商购进这批海鱼100千克,试估计这批海鱼有多少条(同一组中的数据用该区间的中点值作代表);
(Ⅱ)根据市场行情,该海鱼按重量可分为三个等级,如下表:
等级 | 一等品 | 二等品 | 三等品 |
重量(g) | [165,185] | [155,165) | [145,155) |
若经销商以这50条海鱼的样本数据来估计这批海鱼的总体数据,视频率为概率.现从这批海鱼中随机抽取3条,记抽到二等品的条数为X,求x的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com