
【题目】9件产品中,有4件一等品,3件二等品,2件三等品,现在要从中抽出4件产品来检查,至少有两件一等品的抽取方法是( )
A.C C
B.C +C +C
C.C +C
D.C C +C C +C C
 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
【题目】为了分析某个高三学生的学习状态,对其下一阶段的学习提供指导性建议.现对他前![]() 次考试的数学成绩
次考试的数学成绩![]() 、物理成绩
、物理成绩![]() 进行分析.下面是该生
进行分析.下面是该生![]() 次考试的成绩.
次考试的成绩.
88 | 83 | 117 | 92 | 108 | 100 | 112 | |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
(1)他的数学成绩与物理成绩哪个更稳定?请给出你的理由;
(2)已知该生的物理成绩![]() 与数学成绩
与数学成绩![]() 是线性相关的,若该生的物理成绩达到
是线性相关的,若该生的物理成绩达到![]() 分,请你估计他的数学成绩大约是多少?
分,请你估计他的数学成绩大约是多少?
(参考公式: 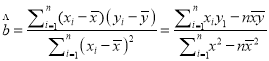 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=exsinx,其中x∈R,e=2.71828…为自然对数的底数. (Ⅰ)求函数f(x)的单调区间;
(Ⅱ)当 ![]() 时,f(x)≥kx,求实数k的取值范围.
时,f(x)≥kx,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y= ![]() 的定义域为M,那么( )
的定义域为M,那么( )
A.{x|x>﹣1且x≠0}
B.{x|x>﹣1}
C.M={x|x<﹣1或x>0}
D.M={x|x<﹣1或﹣1<x<0或x>0}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2-lnx。
(Ⅰ)当a=![]() 时,判断f(x)的单调性;(Ⅱ)设f(x)≤x3+4x-lnx,在定义域内恒成立,求a的取值范围。
时,判断f(x)的单调性;(Ⅱ)设f(x)≤x3+4x-lnx,在定义域内恒成立,求a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ax2﹣(2a+1)x+2lnx(a≥0)
ax2﹣(2a+1)x+2lnx(a≥0)
(1)当a=0时,求f(x)的单调区间;
(2)求y=f(x)在区间(0,2]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=ax3+bx2+cx的极小值为﹣8,其导函数y=f′(x)的图象经过点 ![]() ,如图所示,
,如图所示, 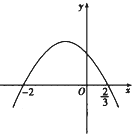
(1)求f(x)的解析式;
(2)若对x∈[﹣3,3]都有f(x)≥m2﹣14m恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com