
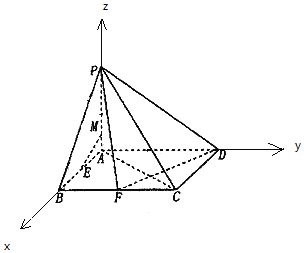
【题目】四棱锥P-ABCD的底面是边长为2的正方形,PA⊥平面ABCD,E,F分别为线段AB,BC的中点.
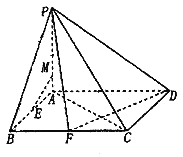
(1)线段AP上一点M,满足![]() ,求证:EM∥平面PDF;
,求证:EM∥平面PDF;
(2)若PB与平面ABCD所成的角为45°,求二面角A-PD-F的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)建立空间直角坐标系,利用![]() ·
·![]() =0,即可证明EM∥平面PDF;
=0,即可证明EM∥平面PDF;
(2)求出平面PDF和平面PAD的一个法向量,利用向量的夹角公式,即可求解二面角的余弦值.
(1)由题意,以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
设PA=a,则A(0,0,0),M(0,0,![]() ),P(0,0,a),F(2,1,0),D(0,2,0),
),P(0,0,a),F(2,1,0),D(0,2,0),
E(1,0,0),所以![]() =(-1,0,
=(-1,0,![]() ),
),![]() =(2,1,-a),
=(2,1,-a),![]() =(0,2,-a),
=(0,2,-a),
设平面PDF的法向量![]() =(x,y,z),
=(x,y,z),
则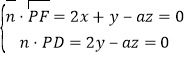 ,取z=2,得
,取z=2,得![]() =(
=(![]() ,a,2),
,a,2),
∵![]() ·
·![]() =-
=-![]() +2×
+2×![]() =0,EM
=0,EM![]() 平面PDF,∴EM∥平面PDF.
平面PDF,∴EM∥平面PDF.
(2)因为PB与平面ABCD所成的角为45°,可得PA=AB=2,
所以P(0,0,2),D(0,2,0),F(2,1,0),
所以![]() =(0,2,-2),
=(0,2,-2),![]() =(2,1,0),
=(2,1,0),
设平面PDF的法向量为![]() =(x,y,z),
=(x,y,z),
则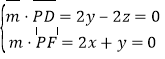 ,取y=1,得
,取y=1,得![]() =(
=(![]() ,1,1),
,1,1),
又由平面PAD的法向量![]() =(1,0,0),
=(1,0,0),
设二面角A-PD-F的平面角为θ,则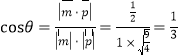 ,
,
∴二面角A-PD-F的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某课题小组共10人,已知该小组外出参加交流活动次数为1,2,3的人数分别为3,3, 4,现从这10人中随机选出2人作为该组代表参加座谈会.
(1)记“选出2人外出参加交流活动次数之和为4”为事件A,求事件A发生的概率;
(2)设X为选出2人参加交流活动次数之差的绝对值,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着国家二孩政策的全面放开,为了调查一线城市和非一线城市的二孩生育意愿,某机构用简单随机抽样方法从不同地区调查了100位育龄妇女,结果如下表.
非一线城市 | 一线城市 | 总计 | |
愿生 | 45 | 20 | 65 |
不愿生 | 13 | 22 | 35 |
总计 | 58 | 42 | 100 |
附表:
|
|
|
|
|
|
|
|
|
|
由![]() 算得,
算得,![]() ,
,
参照附表,得到的正确结论是
A. 在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别有关”
B. 在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别无关”
C. 有99%以上的把握认为“生育意愿与城市级别有关”
D. 有99%以上的把握认为“生育意愿与城市级别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a=(sinx,cosx),b=(sinx,sinx),f(x)=2a·b.
(1)求f(x)的最小正周期和最大值;
(2)若g(x)=f(x),x∈![]() ,画出函数y=g(x)的图象,讨论y=g(x)-m(m∈R)的零点个数.
,画出函数y=g(x)的图象,讨论y=g(x)-m(m∈R)的零点个数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了适应高考改革,某中学推行“创新课堂”教学.高一平行甲班采用“传统教学”的教学方式授课,高一平行乙班采用“创新课堂”的教学方式授课,为了比较教学效果,期中考试后,分别从两个班中各随机抽取![]() 名学生的成绩进行统计分析,结果如下表:(记成绩不低于
名学生的成绩进行统计分析,结果如下表:(记成绩不低于![]() 分者为“成绩优秀”)
分者为“成绩优秀”)
分数 |
|
|
|
|
|
|
|
甲班频数 |
|
|
|
|
|
|
|
乙班频数 |
|
|
|
|
|
|
|
(Ⅰ)由以上统计数据填写下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“成绩优秀与教学方式有关”?
以上的把握认为“成绩优秀与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(Ⅱ)现从上述样本“成绩不优秀”的学生中,抽取![]() 人进行考核,记“成绩不优秀”的乙班人数为
人进行考核,记“成绩不优秀”的乙班人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
参考公式:![]() ,其中
,其中![]() .
.
临界值表
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下四个说法:
①残差点分布的带状区域的宽度越窄相关指数越小
②在刻画回归模型的拟合效果时,相关指数![]() 的值越大,说明拟合的效果越好;
的值越大,说明拟合的效果越好;
③在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均增加
平均增加![]() 个单位;
个单位;
④对分类变量![]() 与
与![]() ,若它们的随机变量
,若它们的随机变量![]() 的观测值
的观测值![]() 越小,则判断“
越小,则判断“![]() 与
与![]() 有关系”的把握程度越大.
有关系”的把握程度越大.
其中正确的说法是![]()
A. ①④B. ②④C. ①③D. ②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】CPI是居民消费价格指数(consumer price index)的简称.居民消费价格指数,是一个反映居民家庭一般所购买的消费品价格水平变动情况的宏观经济指标.右图是根据统计局发布的2018年1月—7月的CPI 同比增长与环比增长涨跌幅数据绘制的折线图.(注:2018 年2月与2017年2月相比较,叫同比;2018年2 月与2018年1月相比较,叫环比)根据该折线图,则下列结论错误的是( )
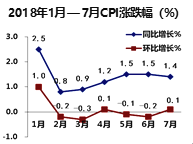
A. 2018年1月—7月CPI 有涨有跌
B. 2018年2月—7月CPI 涨跌波动不大,变化比较平稳
C. 2018年1月—7月分别与2017年1月一7月相比较,1月CPI 涨幅最大
D. 2018年1月—7月分别与2017年1月一7月相比较,CPI 有涨有跌
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点P(3,4)
(1)它在y轴上的截距是在x轴上截距的2倍,求直线l的方程.
(2)若直线l与![]() 轴,
轴,![]() 轴的正半轴分别交于点
轴的正半轴分别交于点![]() ,求
,求![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com