Question

对于函数f(x)=bx³+ax²-3x.

（1）若f(x)在x=1和x=3处取得极值，且f(x)的图象上每一点的切线的斜率均不超过2sintcost-2cos²t+,试求实数t的取值范围；

（2）若f(x）为实数集R上的单调函数，且b≥-1,设点P的坐标为（a,b)，试求出点P的轨迹所围成的图形的面积S.

Answer 1

（1）k+≤t≤k+,k∈Z（2）面积为S=(1-a²)da=4

解析:

  （1）由f(x)=bx³+ax²-3x,

则f′(x)=3bx²+2ax-3,

∵f（x）在x=1和x=3处取得极值，

∴x=1和x=3是f′(x)=0的两个根且b≠0.

.

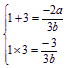
∴f′(x)=-x²+4x-3.

∵f(x)的图象上每一点的切线的斜率不超过

2sintcost-2cos²t+,

∴f′(x)≤2sintcost-2cos²t+对x∈R恒成立，

而f′(x)=-(x-2)²+1,其最大值为1.

故2sintcost-2cos²t+≥1

2sin(2t-)≥12k+≤2t-≤2k+,k∈Z

k+≤t≤k+,k∈Z.

（2）当b=0时，由f(x)在R上单调，知a=0.

当b≠0时，由f(x)在R上单调

f′(x)≥0恒成立，或者f′(x)≤0恒成立.

∵f′(x)=3bx²+2ax-3,

∴Δ=4a²+36b≤0可得b≤-a².

从而知满足条件的点P（a,b)在直角坐标平面aOb上形成的轨迹所围成的图形是由曲线b=-a²与直线b=-1所围成的封闭图形，

其面积为S=(1-a²)da=4.