
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为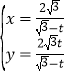 (
(![]() 为参数,且
为参数,且![]() ),以坐标原点为极点,
),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将曲线![]() 的参数方程化为普通方程,并将曲线
的参数方程化为普通方程,并将曲线![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)求曲线![]() 与曲线
与曲线![]() 交点的极坐标
交点的极坐标![]() .
.
科目:高中数学 来源: 题型:
【题目】已知一元二次函数![]() 的图像与
的图像与![]() 轴有两个不同的交点,其中一个交点的坐标为
轴有两个不同的交点,其中一个交点的坐标为![]() 且当
且当![]() 时,恒有
时,恒有![]()
(1)求出不等式![]() 的解(用
的解(用![]() 表示);
表示);
(2)若以二次函数的图像与坐标轴的三个交点为顶点的三角形的面积为8,求![]() 的取值范围;
的取值范围;
(3)若不等式![]() 对所有
对所有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线C的顶点在坐标原点,对称轴为x轴,抛物线C过点A(4,4),过抛物线C的焦点F作倾斜角等于45°的直线l,直线l交抛物线C于M、N两点.
(1)求抛物线C的方程;
(2)求线段MN的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校计划利用周五下午第一、二、三节课举办语文、数学、英语、理综4科的专题讲座,每科一节课,每节至少有一科,且数学、理综不安排在同一节,则不同的安排方法共有( )
A. 6种 B. 24种 C. 30种 D. 36种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解学生使用手机的情况,分别在高一和高二两个年级各随机抽取了100名学生进行调查.下面是根据调查结果绘制的学生日均使用手机时间的频数分布表和频率分布直方图,将使用手机时间不低于80分钟的学生称为“手机迷”.

高一学生日均使用手机时间的频数分布表
时间分组 | 频数 |
[0,20) | 12 |
[20,40) | 20 |
[40,60) | 24 |
[60,80) | 18 |
[80,100) | 22 |
[100,120] | 4 |
(1)将频率视为概率,估计哪个年级的学生是“手机迷”的概率大?请说明理由.
(2)在高二的抽查中,已知随机抽到的女生共有55名,其中10名为“手机迷”.根据已知条件完成下面的2×2列联表,并据此资料你有多大的把握认为“手机迷”与性别有关?
非手机迷 | 手机迷 | 合计 | |
男 | |||
女 | |||
合计 |
附:随机变量 (其中
(其中![]() 为样本总量).
为样本总量).
参考数据 |
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只红蚂蚁与一只黑蚂蚁在一个单位圆(半径为1的圆)上爬动,若两只蚂蚁均从点A(1,0)同时逆时针匀速爬动,若红蚂蚁每秒爬过α角,黑蚂蚁每秒爬过β角(其中0°<α<β<180°),如果两只蚂蚁都在第14秒时回到A点,并且在第2秒时均位于第二象限,求α,β的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以直角坐标系的原点为极点,以
为参数),以直角坐标系的原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,已知直线
轴的正半轴为极轴建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)若![]() 与曲线
与曲线![]() 相切,且
相切,且![]() 与坐标轴交于
与坐标轴交于![]() 两点,求以
两点,求以![]() 为直径的圆的极坐标方程.
为直径的圆的极坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com