
如图,抛物线 与x轴交于A、B两点,与y轴交于点C,连接BC、AC。
与x轴交于A、B两点,与y轴交于点C,连接BC、AC。

(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合)。过点E作直线l平行BC,交AC于点D。设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留 )。
)。
(1)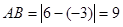 ,
,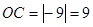 ,(2)
,(2)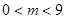 (3)
(3)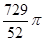
【解析】
试题分析:解:(1)令y=0,即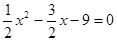 ,
,
整理得 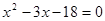 ,
,
解得: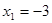 ,
,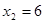 ,
,
∴ A(—3,0),B(6,0)
令x = 0,得y = —9,
∴ 点C(0,—9)
∴ 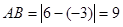 ,
,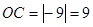 ,
3分
,
3分
(2) ,
,
∵ l∥BC,
∴ △ADE∽△ACB,
∴ 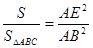 ,即
,即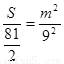
∴ 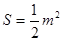 ,其中
,其中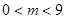 。
6分
。
6分
(3) ,
,
∵ 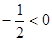
∴ 当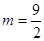 时,S△CDE取得最大值,且最大值是
时,S△CDE取得最大值,且最大值是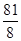 。
。
这时点E(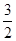 ,0),
,0),
∴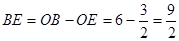 ,
, ,
,
作EF⊥BC,垂足为F,
∵∠EBF=∠CBO,∠EFB=∠COB,
∴△EFB∽△COB,
∴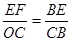 ,即
,即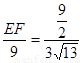
∴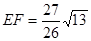 ,
,
∴ ⊙E的面积为: 。
。
答:以点E为圆心,与BC相切的圆的面积为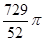 。
11分
。
11分
考点:二次函数的性质、相似三角形的性质
点评:该题主要考查了二次函数的性质、相似三角形的性质、图形面积的求法等综合知识.在解题时,要多留意图形之间的关系,有些时候将所求问题进行时候转化可以大大的降低解题的难度.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
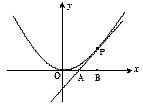 如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,定点B的坐标为(2,0).
如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,定点B的坐标为(2,0).| AB |
| BM |
| 2 |
| AM |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1、F2为焦点,离心率e=
如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1,焦点为F2;以F1、F2为焦点,离心率e=| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,设抛物线C1:y2=4mx(m>0)的焦点为F2,且其准线与x轴交于F1,以F1,F2为焦点,离心率e=
如图所示,设抛物线C1:y2=4mx(m>0)的焦点为F2,且其准线与x轴交于F1,以F1,F2为焦点,离心率e=| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com