
分析 由已知中数列{an}满足${a_1}=1,{a_{n+1}}=\frac{1}{2}{a_n}+1(n∈N*)$,通过计算a2,a3,a4,分析分子分母的变化规律,可得数列的通项公式.
解答 解:∵数列{an}满足${a_1}=1,{a_{n+1}}=\frac{1}{2}{a_n}+1(n∈N*)$,
当n=1时,${a}_{2}=\frac{1}{2}{a}_{1}+1$=$\frac{3}{2}$,
当n=2时,${a}_{3}=\frac{1}{2}{a}_{2}+1$=$\frac{7}{4}$,
当n=1时,${a}_{4}=\frac{1}{2}{a}_{3}+1$=$\frac{15}{8}$,
…
归纳可得:an=$\frac{{{2^n}-1}}{{{2^{n-1}}}}$.
故答案为:$\frac{{{2^n}-1}}{{{2^{n-1}}}}$
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x∈M是x∈N的充分不必要条件 | B. | x∈M是x∈N的必要不充分条件 | ||
| C. | x∈M是x∈N 的充分必要条件 | D. | x∈M是x∈N的既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 是等比数列但不是等差数列 | B. | 是等差数列但不是等比数列 | ||
| C. | 既是等差数列又是等比数列 | D. | 既不是等差数列也不是等比数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A>B | B. | A≥B | C. | A<B | D. | A≤B |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
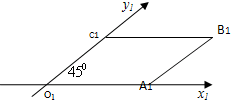 如图,一个正方形OABC在斜二测画法下的直观图是个一条边长为1的平行四边形,则正方形OABC的面积为( )
如图,一个正方形OABC在斜二测画法下的直观图是个一条边长为1的平行四边形,则正方形OABC的面积为( )| A. | 1 | B. | 4 | C. | 1或4 | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com