
【题目】已知f(x)=ax3+bx2+c的图象经过点(0,1),且在x=1处的切线方程是y=x.
(1)求y=f(x)的解析式;
(2)求y=f(x)的单调递增区间.
【答案】
(1)解:f(x)=ax3+bx2+c的图象经过点(0,1),则c=1,
f′(x)=3ax2+2bx,f′(1)=3a+2b=1①,
切点为(1,1),则f(x)=ax3+bx2+c的图象经过点(1,1),
得a+b+1=1②,联立①②解得a=1,b=﹣1,
∴f(x)=x3﹣x2+1
(2)解:f′(x)=3x2﹣2x>0得x<0或x> ![]() ,
,
单调递增区间为(﹣∞,0),( ![]() ,+∞)
,+∞)
【解析】(1)由f(x)=ax3+bx2+c的图象经过点(0,1),得c=1,由导数的几何意义得f′(1)=3a+2b=1①,易求切点(1,1),代入函数解析式可得a+b+1=1②,联立可解;(2)解不等式f′(x)>0可得增区间,注意写成区间形式;
【考点精析】掌握利用导数研究函数的单调性是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


科目:高中数学 来源: 题型:
【题目】如图,已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面,平面ABCD∩平面ABPE=AB,且AB=BP=2,AD=AE=1,AE⊥AB,且AE∥BP. (Ⅰ)设点M为棱PD中点,求证:EM∥平面ABCD;
(Ⅱ)线段PD上是否存在一点N,使得直线BN与平面PCD所成角的正弦值等于 ![]() ?若存在,试确定点N的位置;若不存在,请说明理由.
?若存在,试确定点N的位置;若不存在,请说明理由.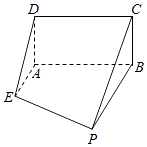
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=xlnx,g(x)=x3+ax2﹣x+2 (Ⅰ)如果函数g(x)的单调递减区间为(﹣ ![]() ,1),求函数g(x)的解析式;
,1),求函数g(x)的解析式;
(Ⅱ)对一切的x∈(0,+∞),2f(x)≤g′(x)+2恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】锐角△ABC中,角A,B,C的对边分别为a,b,c,向量 ![]() ,
, ![]() ,且
,且 ![]() .
.
(1)求角B的大小;
(2)若sinAsinC=sin2B,求a﹣c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,B1B=B1A=AB=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D. 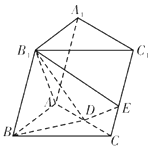
(1)求证:平面ABB1A1⊥平面ABC;
(2)在线段CC1(不含端点)上,是否存在点E,使得二面角E﹣B1D﹣B的余弦值为 ![]() ?若存在,求出
?若存在,求出 ![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com