
【题目】如果对于函数f(x)定义域内任意的两个自变量的值x1,x2,当x1<x2时,都有f(x1)≤f(x2),且存在两个不相等的自变量值y1,y2,使得f(y1)=f(y2),就称f(x)为定义域上的不严格的增函数.则①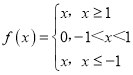 ,②
,②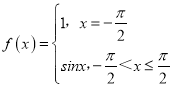 ,③
,③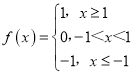 ,④
,④![]() ,四个函数中为不严格增函数的是_____,若已知函数g(x)的定义域、值域分别为A、B,A={1,2,3},BA,且g(x)为定义域A上的不严格的增函数,那么这样的g(x)有_____个.
,四个函数中为不严格增函数的是_____,若已知函数g(x)的定义域、值域分别为A、B,A={1,2,3},BA,且g(x)为定义域A上的不严格的增函数,那么这样的g(x)有_____个.
【答案】①③ 9
【解析】
①③两个函数满足题意,②是严格单调递增的函数,不合题意,④当x1![]() ,x2∈(1,
,x2∈(1,![]() ),f(x1)>f(x2),不合题意;分别列举出满足条件的函数关系即可得解.
),f(x1)>f(x2),不合题意;分别列举出满足条件的函数关系即可得解.
由已知中:函数f(x)定义域内任意的两个自变量的值x1,x2,
当x1<x2时,都有f(x1)≤f(x2),
且存在两个不相等的自变量值y1,y2,使得f(y1)=f(y2),
就称f(x)为定义域上的不严格的增函数.
①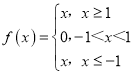 ,满足条件,为定义在R上的不严格的增函数;
,满足条件,为定义在R上的不严格的增函数;
②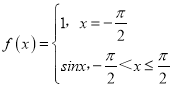 ,当x1
,当x1![]() ,x2∈(
,x2∈(![]() ,
,![]() ),f(x1)>f(x2),故不是不严格的增函数;
),f(x1)>f(x2),故不是不严格的增函数;
③ ,满足条件,为定义在R上的不严格的增函数;
,满足条件,为定义在R上的不严格的增函数;
④![]() ,当x1
,当x1![]() ,x2∈(1,
,x2∈(1,![]() ),f(x1)>f(x2),故不是不严格的增函数;
),f(x1)>f(x2),故不是不严格的增函数;
故已知的四个函数中为不严格增函数的是①③;
∵函数g(x)的定义域、值域分别为A、B,A={1,2,3},BA,且g(x)为定义域A上的不严格的增函数,
则满足条件的函数g(x)有:
g(1)=g(2)=g(3)=1,
g(1)=g(2)=g(3)=2,
g(1)=g(2)=g(3)=3,
g(1)=g(2)=1,g(3)=2,
g(1)=g(2)=1,g(3)=3,
g(1)=g(2)=2,g(3)=3,
g(1)=1,g(2)=g(3)=2,
g(1)=1,g(2)=g(3)=3,
g(1)=2,g(2)=g(3)=3,
故这样的函数共有9个,
故答案为:①③;9.


科目:高中数学 来源: 题型:
【题目】在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转,如图,小卢利用图形的旋转设计某次活动的徽标,他将边长为a的正三角形ABC 绕其中心O逆时针旋转到三角形A1B1C1,且![]() .顺次连结A,A1,B,B1,C,C1,A,得到六边形徽标AA1BB1CC1 .
.顺次连结A,A1,B,B1,C,C1,A,得到六边形徽标AA1BB1CC1 .
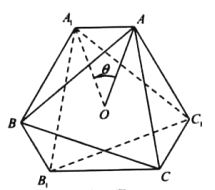
(1)当=![]() 时,求六边形徽标的面积;
时,求六边形徽标的面积;
(2)求六边形徽标的周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A是圆锥的顶点,BD是圆锥底面的直径,C是底面圆周上一点,AC=BD=2,BC=1,点M在线段BD上,且BM![]() ,平面ABC和平面ACD将圆锥截去部分后的几何体如图所示.
,平面ABC和平面ACD将圆锥截去部分后的几何体如图所示.
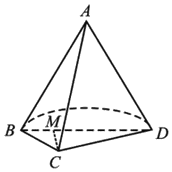
(1)求证:CM⊥AD;
(2)求AC与底面所成的角;
(3)求该几何体的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com