
ЁОЬтФПЁПДгФГДѓбЇвЛФъМЖХЎЩњжаЃЌбЁШЁЩэИпЗжБ№ЪЧ150cmЁЂ155cmЁЂ160cmЁЂ165cmЁЂ170cmЕФбЇЩњИївЛУћЃЌЦфЩэИпКЭЬхжиЪ§ОнШчБэЫљЪОЃК
ЩэИп/cmЃЈxЃЉ | 150 | 155 | 160 | 165 | 170 |
Ьхжи/kgЃЈyЃЉ | 43 | 46 | 49 | 51 | 56 |
ЃЈ1ЃЉЧѓyЙигкxЕФЯпадЛиЙщЗНГЬЃЛ
ЃЈ2ЃЉРћгУЃЈ1ЃЉжаЕФЛиЙщЗНГЬЃЌМЦЫуЩэИпЮЊ168cmЪБЃЌЬхжиЕФЙРМЦжЕ ![]() ЮЊЖрЩйЃП
ЮЊЖрЩйЃП
ВЮПМЙЋЪНЃКЯпадЛиЙщЗНГЬ ![]() =
= ![]() x+
x+ ![]() ЃЌЦфжа
ЃЌЦфжа ![]() =
=  =
= 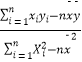 ЃЌ
ЃЌ ![]() =
= ![]() Љ
Љ ![]()
![]() ЃЎ
ЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКгЩвбжЊЪ§ОнЃЌПЩЕУ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ 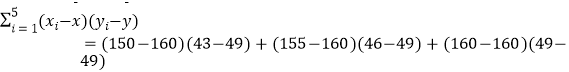
ЃЈ165Љ160ЃЉЃЈ51Љ49ЃЉ+ЃЈ170Љ160ЃЉЃЈ56Љ49ЃЉ=155ЃЌ 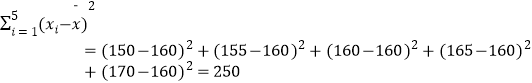
Ёр 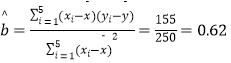 ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
ЁрyЙигкxЕФЯпадЛиЙщЗНГЬЮЊy=0.62xЉ50.2
ЃЈ2ЃЉНтЃКгЩЃЈ1ЃЉжЊЃЌЕБx=168ЪБЃЌ ![]() ЃЈkgЃЉ
ЃЈkgЃЉ
вђДЫЃЌЕБЩэИпЮЊ168cmЪБЃЌЬхжиЕФЙРМЦжЕ ![]() ЮЊ53.96kg
ЮЊ53.96kg
ЁОНтЮіЁПЃЈ1ЃЉЯШЧѓГіКсБъКЭзнБъЕФЦНОљЪ§ЃЌЕУЕНетзщЪ§ОнЕФбљБОжааФЕуЃЌРћгУзюаЁЖўГЫЗЈЧѓГіЯпадЛиЙщЗНГЬЕФЯЕЪ§ЃЌДњШыбљБОжааФЕуЧѓГіaЕФжЕЃЌаДГіЯпадЛиЙщЗНГЬЃЛЃЈ2ЃЉгЩЛиЙщжБЯпЗНГЬЃЌМЦЫуЕБx=168cmЪБЃЌМДПЩЧѓЕУЬхжиЕФЙРМЦжЕ ![]() ЃЎ
ЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЭЈбЖЙЋЫОашвЊдкШ§НЧаЮЕиДјOACЧјгђФкНЈдьМзЁЂввСНжжЭЈаХаХКХМгЧПжазЊеОЃЌМзжазЊеОНЈдкЧјгђBOCФкЃЌввжазЊеОНЈдкЧјгђAOBФкЃЎЗжНчЯпOBЙЬЖЈЃЌЧвOB=ЃЈ1+ ![]() ЃЉАйУзЃЌБпНчЯпACЪМжеЙ§ЕуBЃЌБпНчЯпOAЁЂOCТњзуЁЯAOC=75ЁуЃЌЁЯAOB=30ЁуЃЌЁЯBOC=45ЁуЃЎЩшOA=xЃЈ3ЁмxЁм6ЃЉАйУзЃЌOC=yАйУзЃЎ
ЃЉАйУзЃЌБпНчЯпACЪМжеЙ§ЕуBЃЌБпНчЯпOAЁЂOCТњзуЁЯAOC=75ЁуЃЌЁЯAOB=30ЁуЃЌЁЯBOC=45ЁуЃЎЩшOA=xЃЈ3ЁмxЁм6ЃЉАйУзЃЌOC=yАйУзЃЎ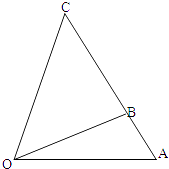
ЃЈ1ЃЉЪдНЋyБэЪОГЩxЕФКЏЪ§ЃЌВЂЧѓГіКЏЪ§yЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕБxШЁКЮжЕЪБЃПећИіжазЊеОЕФеМЕиУцЛ§SЁїOACзюаЁЃЌВЂЧѓГіЦфУцЛ§ЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
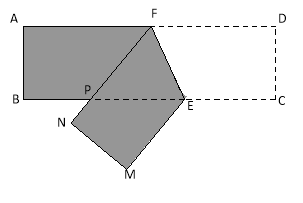
ЁОЬтФПЁПЁО2017ФЯЭЈвЛФЃЁПЃЈБОЬтТњЗж16ЗжЃЉШчЭМЃЌФГЛњаЕГЇвЊНЋГЄ6mЃЌПэ2mЕФГЄЗНаЮЬњЦЄABCDНјааВУМєЁЃвбжЊЕуFЮЊADЕФжаЕуЃЌЕуEдкБпBCЩЯЃЌВУМєЪБЯШНЋЫФБпаЮCDFEбижБЯпEFЗелЕНMNFEДІЃЈЕуCЃЌDЗжБ№ТфдкжБЯпBCЯТЗНЕуMЃЌNДІЃЌFNНЛБпBCгкЕуPЃЉЃЌдйбижБЯпPEВУМєЁЃ
ЃЈ1ЃЉЕБ![]() ЪБЃЌЪдХаЖЯЫФБпаЮMNPEЕФаЮзДЃЌВЂЧѓЦфУцЛ§ЃЛ
ЪБЃЌЪдХаЖЯЫФБпаЮMNPEЕФаЮзДЃЌВЂЧѓЦфУцЛ§ЃЛ
ЃЈ2ЃЉШєЪЙВУМєЕУЕНЕФЫФБпаЮMNPEУцЛ§зюДѓЃЌЧыИјГіВУМєЗНАИЃЌВЂЫЕУїРэгЩЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁО2017СЩФўААЩНЪазюКѓвЛДЮФЃЁПШчЭМЫљЪО,дкШ§РтзЖ![]() жа,ВрУц
жа,ВрУц![]() ,
, ![]() ЪЧШЋЕШЕФжБНЧШ§НЧаЮ,
ЪЧШЋЕШЕФжБНЧШ§НЧаЮ, ![]() ЪЧЙЋЙВЕФаББпЧв
ЪЧЙЋЙВЕФаББпЧв![]() ,
, ![]() ,СэвЛВрУц
,СэвЛВрУц![]() ЪЧе§Ш§НЧаЮ.
ЪЧе§Ш§НЧаЮ.

ЃЈ1ЃЉЧѓжЄЃК ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєдкЯпЖЮ![]() ЩЯДцдквЛЕу
ЩЯДцдквЛЕу![]() ,ЪЙ
,ЪЙ![]() гыЦНУц
гыЦНУц![]() ГЩ
ГЩ![]() НЧ,ЪдЧѓЖўУцНЧ
НЧ,ЪдЧѓЖўУцНЧ![]() ЕФгрЯвжЕ.
ЕФгрЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊSnЮЊЕШВюЪ§Са{an}ЕФЧАnЯюКЭЃЌЧвa1=Љ15ЃЌS5=Љ55ЃЎ
ЃЈ1ЃЉЧѓЪ§Са{an}ЕФЭЈЯюЙЋЪНЃЛ
ЃЈ2ЃЉШєВЛЕШЪНSnЃОtЖдгкШЮвтЕФnЁЪN*КуГЩСЂЃЌЧѓЪЕЪ§tЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
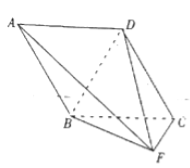
ЁОЬтФПЁПЁО2017ЫФДЈуђжнЫФеяЁПШчЭМЃЌЦНУц![]() ЦНУц
ЦНУц![]() ЃЌЫФБпаЮ
ЃЌЫФБпаЮ![]() ЪЧСтаЮЃЌ
ЪЧСтаЮЃЌ ![]() .
.
ЃЈ1ЃЉЧѓжЄЃК ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧвжБЯп
ЃЌЧвжБЯп![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЮЊ
ЫљГЩНЧЮЊ![]() ЃЌЧѓЖўУцНЧ
ЃЌЧѓЖўУцНЧ![]() ЕФЦНУцНЧЕФгрЯвжЕ.
ЕФЦНУцНЧЕФгрЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
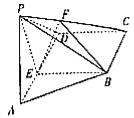
ЁОЬтФПЁП ЁО2017НЮї4дТжЪМьЁПШчЭМЃЌЫФРтзЖ![]() жаЃЌВрУц
жаЃЌВрУц![]() ЕзУц
ЕзУц![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ,
, ![]() ЃЌ
ЃЌ ![]() ЃЌЕу
ЃЌЕу![]() дкРт
дкРт![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЃЌЕу
ЃЌЕу![]() дкРт
дкРт![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЦНУц
ЦНУц![]() .
.
ЃЈ1ЃЉЧѓжЄЃК ![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓЖўУцНЧ![]() ЕФгрЯвжЕ.
ЕФгрЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпCЃКy2=2pxЃЈpЃО0ЃЉЕФНЙЕуЮЊFЃЌШєЙ§ЕуFЧваБТЪЮЊ1ЕФжБЯпгыХзЮяЯпЯрНЛгкMЃЌNСНЕуЃЌЧв|MN|=8ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпCЕФЗНГЬЃЛ
ЃЈ2ЃЉЩшжБЯпlЮЊХзЮяЯпCЕФЧаЯпЃЌЧвlЁЮMNЃЌPЮЊlЩЯвЛЕуЃЌЧѓ ![]() ЕФзюаЁжЕЃЎ
ЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊвЛИіПкДќгаmИіАзЧђЃЌnИіКкЧђЃЈm,n![]()
![]() ,n
,n![]() 2ЃЉ,етаЉЧђГ§беЩЋЭтШЋВПЯрЭЌЁЃЯжНЋПкДќжаЕФЧђЫцЛњЕФж№ИіШЁГіЃЌВЂЗХШыШчЭМЫљЪОЕФБрКХЮЊ1,2,3ЃЌЁЁЃЌm+nЕФГщЬыФкЃЌЦфжаЕкkДЮШЁЧђЗХШыБрКХЮЊkЕФГщЬыЃЈk=1,2,3ЃЌЁЁЃЌm+nЃЉ.
2ЃЉ,етаЉЧђГ§беЩЋЭтШЋВПЯрЭЌЁЃЯжНЋПкДќжаЕФЧђЫцЛњЕФж№ИіШЁГіЃЌВЂЗХШыШчЭМЫљЪОЕФБрКХЮЊ1,2,3ЃЌЁЁЃЌm+nЕФГщЬыФкЃЌЦфжаЕкkДЮШЁЧђЗХШыБрКХЮЊkЕФГщЬыЃЈk=1,2,3ЃЌЁЁЃЌm+nЃЉ.
![]()
ЃЈ1ЃЉЪдЧѓБрКХЮЊ2ЕФГщЬыФкЗХЕФЪЧКкЧђЕФИХТЪp;
ЃЈ2ЃЉЫцЛњБфСПxБэЪОзюКѓвЛИіШЁГіЕФКкЧђЫљдкГщЬыБрКХЕФЕЙЪ§ЃЌE(x)ЪЧxЕФЪ§бЇЦкЭћЃЌжЄУї ![]()
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com