
【题目】已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.
(1)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(2)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.用X表示抽取的3人中睡眠充足的员工人数,求随机变量X的分布列与数学期望.
科目:高中数学 来源: 题型:
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.如图是甲流水线样本的频数分布表和乙流水线样本的频率分布直方图.
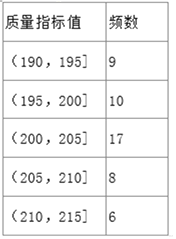
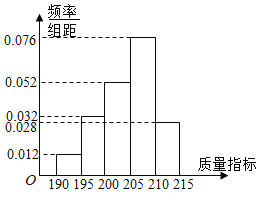
(1)根据频率分布直方图,估计乙流水线生产的产品该质量指标值的中位数;
(2)若将频率视为概率,某个月内甲、乙两条流水线均生产了5000件产品,则甲、乙两条流水线分别生产出不合格品约多少件?
(3)根据已知条件完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
的把握认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
甲流水线 | 乙流水线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:![]() ,其中
,其中![]() .
.
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三角形ABE与菱形ABCD所在的平面互相垂直,![]() ,
,![]() ,M是AB的中点,N是CE的中点.
,M是AB的中点,N是CE的中点.
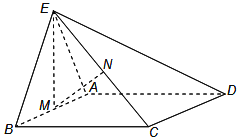
(1)求证:![]() ;
;
(2)求证:![]() 平面ADE;
平面ADE;
(3)求点A到平面BCE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .直线
.直线![]() ,
,![]() 相交于点
相交于点![]() ,且它们的斜率之积是
,且它们的斜率之积是![]() .记点
.记点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求![]() 的方程.
的方程.
(Ⅱ)已知直线![]() ,
,![]() 分别交直线
分别交直线![]() 于点
于点![]() ,
,![]() ,轨迹
,轨迹![]() 在点
在点![]() 处的切线与线段
处的切线与线段![]() 交于点
交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在![]() 中,
中, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() .将
.将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,如图2.
,如图2.
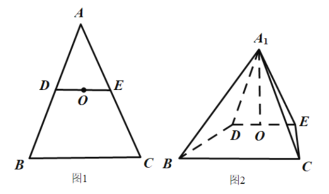
(1)求证:![]() ;
;
(2)求直线![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com