
【题目】已知正三角形ABC边长为2,将它沿高AD翻折,使点B与点C间的距离为 ![]() ,此时四面体ABCD的外接球的表面积为 .
,此时四面体ABCD的外接球的表面积为 .
【答案】7π
【解析】解:根据题意可知三棱锥B﹣ACD的三条侧棱BD⊥AD、DC⊥DA,底面是等腰直角三角形,它的外接球就是它扩展为三棱柱的外接球,求出三棱柱的底面中心连线的中点到顶点的距离,就是球的半径,
三棱柱ABC﹣A1B1C1的中,底面边长为1,1, ![]() ,
,
由题意可得:三棱柱上下底面中点连线的中点,到三棱柱顶点的距离相等,说明中心就是外接球的球心,
∴三棱柱ABC﹣A1B1C1的外接球的球心为O,外接球的半径为r,
棱柱的高为 ![]() ,球心到底面的距离为
,球心到底面的距离为 ![]() ,
,
三棱柱中,底面△BDC,BD=CD=1,BC= ![]() ,∴∠BDC=120°,∴△BDC的外接圆的半径为:
,∴∠BDC=120°,∴△BDC的外接圆的半径为: ![]() =1
=1
∴球的半径为r= ![]() =
= ![]() .
.
外接球的表面积为:4πr2=7π.
故答案为:7π.
三棱锥B﹣ACD的三条侧棱BD⊥AD、DC⊥DA,底面是等腰直角三角形,它的外接球就是它扩展为三棱柱的外接球,求出正三棱柱的底面中心连线的中点到顶点的距离,就是球的半径,然后求球的表面积.


科目:高中数学 来源: 题型:
【题目】某商品要了解年广告费![]() (单位:万元)对年销售额
(单位:万元)对年销售额![]() (单位:万元)的影响,对近4年的年广告费
(单位:万元)的影响,对近4年的年广告费![]() 和年销售额
和年销售额![]() 数据作了初步整理,得到下面的表格:
数据作了初步整理,得到下面的表格:

用广告费作解释变量,年销售额作预报变量,若认为![]() 适宜作为年销售额
适宜作为年销售额![]() 关于年广告费
关于年广告费![]() 的回归方程类型,则
的回归方程类型,则
(1)根据表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)已知商品的年利润![]() 与
与![]() 的关系式为
的关系式为![]() .根据(1)的结果,年广告费
.根据(1)的结果,年广告费![]() 约为何值时(小数点后保留两位),年利润的预报值最大?
约为何值时(小数点后保留两位),年利润的预报值最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
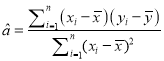 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别是正方体
分别是正方体![]() 的棱
的棱![]() 上两点,且
上两点,且![]() ,给出下列四个命题:①三棱锥
,给出下列四个命题:①三棱锥![]() 的体积为定值;②异面直线
的体积为定值;②异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ;③
;③![]() 平面
平面![]() ;④直线
;④直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .其中正确的命题为( )
.其中正确的命题为( )
A. ①② B. ②③ C. ①②④ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国许多省市雾霾天气频发,为增强市民的环境保护意识,某市面向全市征召![]() 名义务宣传志愿者,成立环境保护宣传组织,现把该组织的成员按年龄分成
名义务宣传志愿者,成立环境保护宣传组织,现把该组织的成员按年龄分成![]() 组第
组第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示,已知第
,得到的频率分布直方图如图所示,已知第![]() 组有
组有![]() 人.
人.

(1)求该组织的人数;
(2)若在第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 名志愿者参加某社区的宣传活动,应从第
名志愿者参加某社区的宣传活动,应从第![]() 组各抽取多少名志愿者?
组各抽取多少名志愿者?
(3)在(2)的条件下,该组织决定在这![]() 名志愿者中随机抽取
名志愿者中随机抽取![]() 名志愿者介绍宣传经验,求第
名志愿者介绍宣传经验,求第![]() 组至少有
组至少有![]() 名志愿者被抽中的概率.
名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个自然数若与它的“反序数”相等,这个自然数就称为一个“魔幻数”如数“![]() ”、“
”、“![]() ”都是“魔幻数”在
”都是“魔幻数”在![]() 的元素中,去掉所有的“魔幻数”后,形成一个不含“魔幻数”的子集
的元素中,去掉所有的“魔幻数”后,形成一个不含“魔幻数”的子集![]() ,则
,则![]() 中的元素共有______个.
中的元素共有______个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装厂生产一种服装,每件服装成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,规定当一次订购量超过100件时,每多订购一件,订购的全部服装的出厂单价就降低![]() 元,根据市场调查,销售商一次订购不会超过600件.
元,根据市场调查,销售商一次订购不会超过600件.
(1)设一次订购![]() 件,服装的实际出厂单价为
件,服装的实际出厂单价为![]() 元,写出函数
元,写出函数![]() 的表达式;
的表达式;
(2)当销售商一次订购多少件服装时,该厂获得的利润最大?其最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点P是平行四边形ABCD所在平面外一点,M、N分别是AB、PC的中点.

(1)求证:MN∥平面PAD;
(2)在PB上确定一个点Q,使平面MNQ∥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)在(2,+∞)上单调递减,且y=f(x+2)为偶函数,则关于x的不等式f(2x﹣1)﹣f(x+1)>0的解集为( )
A.(﹣∞,﹣ ![]() )∪(2,+∞)
)∪(2,+∞)
B.(﹣ ![]() ,2)
,2)
C.(﹣∞, ![]() )∪(2,+∞)
)∪(2,+∞)
D.( ![]() ,2)
,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com