
【题目】已知函数![]()
![]() .
.
(1)当![]() 时,判断函数
时,判断函数![]() 的单调性;
的单调性;
(2)若存在![]() ,使得
,使得![]() (
(![]() 是自然对数的底数),求实数
是自然对数的底数),求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 在
在![]() 单调递增;在
单调递增;在![]() 上单调递减;(2)
上单调递减;(2)![]() .
.
【解析】试题分析:(1)依据题设条件先求导再运用导数与函数的单调性之间的关系分析探求;(2)先将不等式进行等价转化,再构造函数运用导数的知识分析探求:
试题解析:
解:(1)![]()
![]() .
.
当![]() 时,
时,![]() ;
;
当![]() 时
时![]() ;当
;当![]() 时
时![]() .
.
故函数![]() 在
在![]() 单调递增;在
单调递增;在![]() 上单调递减.
上单调递减.
(2)因为存在![]() ,使得
,使得![]() 成立,
成立,
而当![]() 时,
时,![]() ,
,
所以只要![]() 即可.
即可.
又因为![]() ,
,![]() ,
,![]() 的变化情况如下表所示:
的变化情况如下表所示:
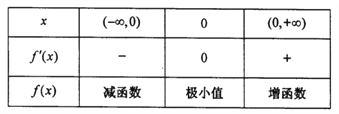
所以![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,所以当
上是增函数,所以当![]() 时,
时,![]() 的最小值
的最小值![]() ,
,![]() 的最大值
的最大值![]() 为
为![]() 和
和![]() 中的最大值.
中的最大值.
因为![]()
![]() ,
,
令![]() ,因为
,因为![]() ,
,
所以![]() 在
在![]() 上是增函数.
上是增函数.
而![]() ,故当
,故当![]() 时,
时,![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() .
.
所以,当![]() 时,
时,![]() ,即
,即![]() ,
,
函数![]() 在
在![]() 上是增函数,解得
上是增函数,解得![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ,
,
函数![]() 在
在![]() 上是减函数,解得
上是减函数,解得![]() .
.
综上可知,所求![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】现在颈椎病患者越来越多,甚至大学生也出现了颈椎病,年轻人患颈椎病多与工作、生活方式有关,某调查机构为了了解大学生患有颈椎病是否与长期过度使用电子产品有关,在遂宁市中心医院随机的对入院的50名大学生进行了问卷调查,得到了如下的4×4列联表:
未过度使用 | 过度使用 | 合计 | |
未患颈椎病 | 15 | 5 | 20 |
患颈椎病 | 10 | 20 | 30 |
合计 | 25 | 25 | 50 |
(1)是否有99.5%的把握认为大学生患颈锥病与长期过度使用电子产品有关?
(2)已知在患有颈锥病的10名未过度使用电子产品的大学生中,有3名大学生又患有肠胃炎,现在从上述的10名大学生中,抽取3名大学生进行其他方面的排查,记选出患肠胃炎的学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据与公式:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某权威机构发布了2014年度“城市居民幸福排行榜”,某市成为本年度城市最“幸福城”.随后,该市某校学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):

(1)指出这组数据的众数和中位数;
(2)若幸福度不低于9.5分,则称该人的幸福度为“极幸福”.求从这16人中随机选取3人,至多有1人是“极幸福”的概率;
(3)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记![]() 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABCA1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,AA1=12,点D是AB的中点.
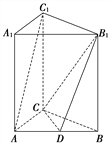
(1)求证:AC⊥B1C;
(2)求证:AC1∥平面CDB1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了了解![]() 两班学生寒假期间观看《中国诗词大会》的时长,分别从这两个班中随机抽取5名学生进行调查,将他们观看的时长(单位:小时)作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
两班学生寒假期间观看《中国诗词大会》的时长,分别从这两个班中随机抽取5名学生进行调查,将他们观看的时长(单位:小时)作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
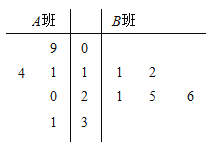
(1)分别求出图中所给两组样本数据的平均值,并据此估计哪个班的学生平均观看的时间较长;
(2)从![]() 班的样本数据中随机抽取一个不超过19的数据记为
班的样本数据中随机抽取一个不超过19的数据记为![]() ,从
,从![]() 班的样本数据中随机抽取一个不超过21的数据记为
班的样本数据中随机抽取一个不超过21的数据记为![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知矩形![]() 的长
的长![]() ,宽
,宽![]() ,将其沿对角线
,将其沿对角线![]() 折起,得到四面体
折起,得到四面体![]() ,
,
如图所示,给出下列结论:
①四面体![]() 体积的最大值为
体积的最大值为![]() ;
;
②四面体![]() 外接球的表面积恒为定值;
外接球的表面积恒为定值;
③若![]() 分别为棱
分别为棱![]() 的中点,则恒有
的中点,则恒有![]() 且
且![]() ;
;
④当二面角![]() 为直二面角时,直线
为直二面角时,直线![]() 所成角的余弦值为
所成角的余弦值为![]() ;
;
⑤当二面角![]() 的大小为
的大小为![]() 时,棱
时,棱![]() 的长为
的长为![]() .
.
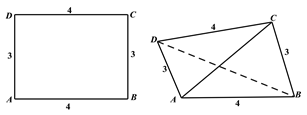
其中正确的结论有____________________(请写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂今年1月、2月、3月生产某种产品的数量分别是1万件、2万件、1.3万件,为了预测以后每个月的产量,以这三个月的产品数量为依据,用一个函数模拟该产品的月产量y与月份x的关系,模拟函数可以选用二次函数或函数y=abx+c(其中a,b,c为常数),已知4月份该产品的产量为1.37万件,请问用以上哪个函数作为模拟函数较好?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com