
【题目】现有长分别为1m、2m、3m的钢管各3根(每根钢管质地均匀、粗细相同附有不同的编号),从中随机抽取2根(假设各钢管被抽取的可能性是均等的),再将抽取的钢管相接焊成笔直的一根.若X表示新焊成的钢管的长度(焊接误差不计).
(1)求X的分布列;
(2)若Y=﹣λ2X+λ+1,E(Y)>1,求实数λ的取值范围.
【答案】
(1)解:X可能的取值为2,3,4,5,6.
则 ![]() ;
;
![]() ;
;
![]()
∴X的分布列为:
X | 2 | 3 | 4 | 5 | 6 |
P |
|
|
|
|
|
(2)解: ![]()
∵Y=﹣λ2X+λ+1,∴E(Y)=﹣λ2E(X)+λ+1=﹣4λ2+λ+1,
∵E(Y)>1,∴ ![]() .
.
∴实数λ的取值范围是 ![]()
【解析】(1)X可能的取值为2,3,4,5,6.求出对应的概率,即可得X的分布列;(2)根据期望的公式进行求解即可.
【考点精析】通过灵活运用离散型随机变量及其分布列,掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 的图象过点(﹣1,2),且在点(﹣1,f(﹣1))处的切线与直线x﹣5y+1=0垂直.
的图象过点(﹣1,2),且在点(﹣1,f(﹣1))处的切线与直线x﹣5y+1=0垂直.
(1)求实数b,c的值;
(2)求f(x)在[﹣1,e](e为自然对数的底数)上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
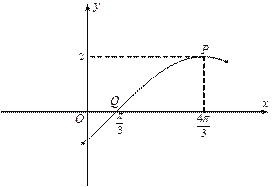
【题目】如图为函数![]() 图像的一部分,其中点
图像的一部分,其中点![]() 是图像的一个最高点,点
是图像的一个最高点,点![]() 是与点
是与点![]() 相邻的图像与
相邻的图像与![]() 轴的一个交点.
轴的一个交点.
⑴ 求函数![]() 的解析式;
的解析式;
⑵ 若将函数![]() 的图像沿
的图像沿![]() 轴向右平移
轴向右平移![]() 个单位,再把所得图像上每一点的横坐标都变为原来的
个单位,再把所得图像上每一点的横坐标都变为原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图像,求函数
的图像,求函数![]() 的单调递增区间.
的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论: ①直线AM与CC1是相交直线;
②直线AM与BN是平行直线;
③直线BN与MB1是异面直线;
④直线AM与DD1是异面直线.
其中正确的结论为(注:把你认为正确的结论的序号都填上).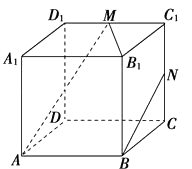
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行四边形ABCD中,A(1,1)、B(7,3)、D(4,6),点M是线段AB的中点线段CM与BD交于点P. 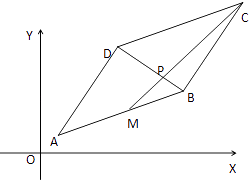
(1)求直线CM的方程;
(2)求点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为R,f(x)= ![]() ,且对任意的x∈R都有f(x+1)=﹣
,且对任意的x∈R都有f(x+1)=﹣ ![]() ,若在区间[﹣5,1]上函数g(x)=f(x)﹣mx+m恰有5个不同零点,则实数m的取值范围是( )
,若在区间[﹣5,1]上函数g(x)=f(x)﹣mx+m恰有5个不同零点,则实数m的取值范围是( )
A.[﹣ ![]() ,﹣
,﹣ ![]() )
)
B.(﹣ ![]() ,﹣
,﹣ ![]() ]
]
C.(﹣ ![]() ,0]
,0]
D.(﹣ ![]() ,﹣
,﹣ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2013年第三季度,国家电网决定对城镇居民用电计费标准作出调整,并根据用电情况将居民分为三类:第一类的用电区间在(0,170],第二类在(170,260],第三类在(260,+∞)(单位:千瓦时).某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图,如图所示.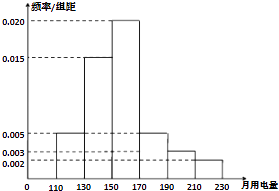
(1)求该小区居民用电量的中位数与平均数;
(2)本月份该小区没有第三类的用电户出现,为鼓励居民节约用电,供电部门决定:对第一类每户奖励20元钱,第二类每户奖励5元钱,求每户居民获得奖励的平均值;
(3)利用分层抽样的方法从该小区内选出5位居民代表,若从该5户居民代表中任选两户居民,求这两户居民用电资费属于不同类型的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长方体ABCD﹣A'B'C'D'中,AB=4,AD=3,AA'=2; 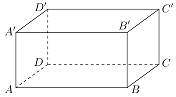
(1)求出异面直线AC'和BD所成角的余弦值;
(2)找出AC'与平面D'DBB'的交点,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com