
【题目】(1)求与椭圆![]() 有公共焦点,并且离心率为
有公共焦点,并且离心率为![]() 的双曲线方程.
的双曲线方程.
(2)已知斜率为1的直线l过椭圆![]() 的右焦点F交椭圆于A、B两点,求弦AB的长.
的右焦点F交椭圆于A、B两点,求弦AB的长.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)根据题意,求出椭圆![]() 的焦点坐标,分析可得要求双曲线的焦点在x轴上,且c=
的焦点坐标,分析可得要求双曲线的焦点在x轴上,且c=![]() ,设其方程为
,设其方程为![]() ﹣
﹣![]() =1,由离心率公式求出a的值,由双曲线的几何性质计算可得b的值,将a、b的值代入双曲线方程即可得答案;(2)设出A、B的坐标,由椭圆方程求出椭圆右焦点坐标,得到A、B所在直线方程,与椭圆方程联立,化为关于x的一元二次方程,利用根与系数的关系可得A、B横坐标的和与积,代入弦长公式求弦AB的长.
=1,由离心率公式求出a的值,由双曲线的几何性质计算可得b的值,将a、b的值代入双曲线方程即可得答案;(2)设出A、B的坐标,由椭圆方程求出椭圆右焦点坐标,得到A、B所在直线方程,与椭圆方程联立,化为关于x的一元二次方程,利用根与系数的关系可得A、B横坐标的和与积,代入弦长公式求弦AB的长.
(1)由椭圆方程为![]() ,知长半轴长
,知长半轴长![]() ,短半轴长
,短半轴长![]() ,
,
焦距的一半![]() ,
,
∴焦点是![]() ,
,![]() ,因此双曲线的焦点也是
,因此双曲线的焦点也是![]() ,
,![]() ,
,
设双曲线方程为![]() ,由题设条件及双曲线的性质,得
,由题设条件及双曲线的性质,得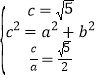 ,解得
,解得![]() ,故所求双曲线的方程为
,故所求双曲线的方程为![]() .
.
(2)设A、B的坐标分别为![]() 、
、![]() .
.
由椭圆的方程知![]() ,
,![]() ,
,![]() ,∴
,∴![]() .
.
直线l的方程为![]() ① 将①代入
① 将①代入![]() ,化简整理得
,化简整理得
![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣10|+|x﹣20|,且满足f(x)<10a+10(a∈R)的解集不是空集.
(Ⅰ)求实数a的取值集合A
(Ⅱ)若b∈A,a≠b,求证aabb>abba .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PB、PD与平面ABCD所成角的正切值依次是1、![]() ,AP=2,E、F依次是PB、PC的中点.
,AP=2,E、F依次是PB、PC的中点.

(1)求证:PB⊥平面AEFD;
(2)求直线EC与平面PAD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的两个焦点F1 , F2和上下两个顶点B1 , B2是一个边长为2且∠F1B1F2为60°的菱形的四个顶点.
(a>b>0)的两个焦点F1 , F2和上下两个顶点B1 , B2是一个边长为2且∠F1B1F2为60°的菱形的四个顶点.
(1)求椭圆C的方程;
(2)过右焦点F2 , 斜率为k(k≠0)的直线与椭圆C相交于E,F两点,A为椭圆的右顶点,直线AE,AF分别交直线x=3于点M,N,线段MN的中点为P,记直线PF2的斜率为k′.求证:kk′为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点为直角坐标系xOy的原点,极轴为x轴的正半轴,两种坐标系中的长度单位相同![]() 直线
直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线C的参数方程为
,曲线C的参数方程为![]() 为参数
为参数![]() ,设直线l与曲线C交于A,B两点.
,设直线l与曲线C交于A,B两点.
![]() 写出直线
写出直线![]() 的普通方程与曲线C的直角坐标方程;
的普通方程与曲线C的直角坐标方程;
![]() 已知点P在曲线C上运动,求点P到直线
已知点P在曲线C上运动,求点P到直线![]() 距离的最大值.
距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某渔业公司年初用81万元购买一艘捕鱼船,第一年各种费用为1万元,以后每年都增加2万元,每年捕鱼收益30万元.
![]() 问第几年开始获利?
问第几年开始获利?
![]() 若干年后,有两种处理方案:方案一:年平均获利最大时,以46万元出售该渔船;
若干年后,有两种处理方案:方案一:年平均获利最大时,以46万元出售该渔船;
方案二:总纯收入获利最大时,以10万元出售该渔船![]() 问:哪一种方案合算?请说明理由.
问:哪一种方案合算?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C的对边分别为a、b、c,a=btanA,且B为钝角.
(1)证明:B﹣A= ![]() ;
;
(2)求sinA+sinC的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com