
科目:高中数学 来源: 题型:
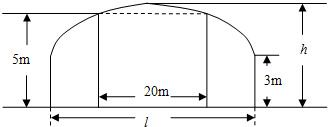
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 野营活动中,学生在平地上用三根斜杆搭建一个正三棱锥形的三脚支架P-ABC(如图)进行野炊训练,将炊事锅看作一个点Q,用吊绳PQ将炊事锅吊起烧水(锅的大小忽略不计).已知PC=130cm,A、B两点间距离为50
野营活动中,学生在平地上用三根斜杆搭建一个正三棱锥形的三脚支架P-ABC(如图)进行野炊训练,将炊事锅看作一个点Q,用吊绳PQ将炊事锅吊起烧水(锅的大小忽略不计).已知PC=130cm,A、B两点间距离为50| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
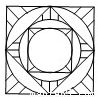
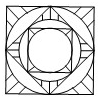 夏都广场地面喷泉的喷头用铸铁防护罩保护,防护罩的图案如图所示,外圈是正方形.正方形的对角线长为2a,在正方形内作一个内切圆;在第一个内切圆内又作一个内接正方形,在正方形内再作第二个内切圆;然后又在第二个内切圆中作内接正方形,在正方形内再作第三个内切圆,…,依此作到第n个内切圆,它的半径是
夏都广场地面喷泉的喷头用铸铁防护罩保护,防护罩的图案如图所示,外圈是正方形.正方形的对角线长为2a,在正方形内作一个内切圆;在第一个内切圆内又作一个内接正方形,在正方形内再作第二个内切圆;然后又在第二个内切圆中作内接正方形,在正方形内再作第三个内切圆,…,依此作到第n个内切圆,它的半径是
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
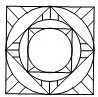 夏都广场地面喷泉的喷头用铸铁防护罩保护,防护罩的图案如图所示,外圈是正方形.正方形的对角线长为2a,在正方形内作一个内切圆;在第一个内切圆内又作一个内接正方形,在正方形内再作第二个内切圆;然后又在第二个内切圆中作内接正方形,在正方形内再作第三个内切圆,…,依此作到第n个内切圆,它的半径是________.
夏都广场地面喷泉的喷头用铸铁防护罩保护,防护罩的图案如图所示,外圈是正方形.正方形的对角线长为2a,在正方形内作一个内切圆;在第一个内切圆内又作一个内接正方形,在正方形内再作第二个内切圆;然后又在第二个内切圆中作内接正方形,在正方形内再作第三个内切圆,…,依此作到第n个内切圆,它的半径是________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com