
【题目】已知函数![]()
(1)当![]() 时,证明
时,证明![]() 在
在![]() 单调递减;
单调递减;
(2)当![]() 时,讨论
时,讨论![]() 的零点个数.
的零点个数.
【答案】(1)见解析;(2)见解析
【解析】
(1)将a的值代入![]() 中,计算导数,构造新函数
中,计算导数,构造新函数![]() ,结合导数,判断
,结合导数,判断![]() 的范围,即可得出
的范围,即可得出![]() 的单调性。(2)构造函数
的单调性。(2)构造函数![]() ,结合导函数,针对a的不同范围,判断
,结合导函数,针对a的不同范围,判断![]() 的零点个数,进而得到
的零点个数,进而得到![]() 的零点个数,即可。
的零点个数,即可。
(1)当![]() 时,
时,![]() ,
,![]() ,
,
令![]() ,则
,则![]() ,
,
![]() ,在
,在![]() 上为减函数,且
上为减函数,且![]() ,
,
令![]() ,得
,得![]() ,所以
,所以![]() 的递增区间为
的递增区间为![]() ,
,
同理,可得![]() 的递减区间为
的递减区间为![]() ,
,
所以![]() 即
即![]() ,
,
故![]() 在
在![]() 单调递减.
单调递减.
(2)由(1)得![]() 时,
时,![]() 在
在![]() 单调递减,又
单调递减,又![]() ,
,
所以![]() 时,
时,![]() 有一个零点.
有一个零点.
因为![]() 定义域为
定义域为![]() ,故
,故![]() 与
与![]() 有相同的零点,
有相同的零点,
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() 时,
时,![]() ,
,![]() 时,
时,![]()
所以![]() ,
,![]() 无零点,
无零点,![]() 也无零点.
也无零点.
当![]() 时,令
时,令![]() ,得
,得![]() 或
或![]()
|
| 1 |
|
|
|
| - | 0 | + | 0 | - |
| ↘ | ↗ | ↘ |
![]() ,
,
当![]() 时,
时,
![]()
当![]() 即
即![]() 时,
时,![]() ,
,
![]()
![]()
故![]() 有一个零点,
有一个零点,![]() 也有有一个零点.
也有有一个零点.
综上可知,当![]() 时,
时,![]() 无零点;
无零点;
当![]() 时,
时,![]() 有一个零点.
有一个零点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列四个命题:
①样本方差反映的是所有样本数据与样本平均值的偏离程度;
②某校高三一级部和二级部的人数分别是m、n,本次期末考试两级部数学平均分分别是a、b,则这两个级部的数学平均分为![]()
③某中学采用系统抽样方法,从该校高一年级全体800名学生中抽50名学生做牙齿健康检查,现将800名学生从001到800进行编号,已知从497--512这16个数中取得的学生编号是503,则初始在第1小组00l~016中随机抽到的学生编号是007.
其中命题正确的个数是( )
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() ⊥底面
⊥底面![]() ,底面
,底面![]() 为等边三角形,
为等边三角形,![]() ,
,![]() ,
, ![]() ,
,![]() 分别为
分别为![]() ,
, ![]() 的中点.
的中点.
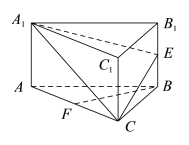
(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成二面角的余弦值;
所成二面角的余弦值;
(3)设平面![]() 与平面
与平面![]() 的交线为
的交线为![]() 求证:
求证:![]() 与平面
与平面![]() 不平行.
不平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知等差数列{an}中,a1=1,a3=﹣3.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{an}的前k项和Sk=﹣35,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:
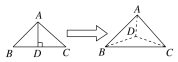
①BD⊥AC;
②△BAC是等边三角形;
③三棱锥D-ABC是正三棱锥;
④平面ADC⊥平面ABC.
其中正确的是( )
A.①②④B.①②③
C.②③④D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分,(1)小问7分,(2)小问5分)
设函数![]()
(1)若![]() 在
在![]() 处取得极值,确定
处取得极值,确定![]() 的值,并求此时曲线
的值,并求此时曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 在
在![]() 上为减函数,求
上为减函数,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为[-1,5],部分对应值如下表,
的定义域为[-1,5],部分对应值如下表, ![]() 的导函数
的导函数![]() 的图象如图所示,下列关于
的图象如图所示,下列关于![]() 的命题:
的命题:

| -1 | 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
①函数![]() 的极大值点为0,4;
的极大值点为0,4;
②函数![]() 在[0,2]上是减函数;
在[0,2]上是减函数;
③如果当![]() 时,
时, ![]() 的最大值是2,那么t的最大值为4;
的最大值是2,那么t的最大值为4;
④当1<a<2时,函数![]() 有4个零点.
有4个零点.
其中正确命题的序号是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com