
【题目】如图,三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,且各棱长均相等,
,且各棱长均相等, ![]() 分别为棱
分别为棱![]() 的中点.
的中点.
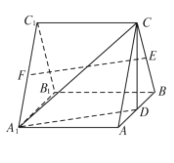
(1)证明![]() 平面
平面![]() ;
;
(2)证明平面![]() 平面
平面![]() ;
;
(3)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】试题分析:(1)连接![]() ,根据平几知识得四边形
,根据平几知识得四边形![]() 为平行四边形,即得
为平行四边形,即得![]() ,根据线面平行判定定理得结论(2)先根据正三角形性质得
,根据线面平行判定定理得结论(2)先根据正三角形性质得![]() ,再根据线面垂直条件得
,再根据线面垂直条件得![]() ,可得
,可得![]() 平面
平面![]() ,最后根据面面垂直判定定理得结论(3)过点
,最后根据面面垂直判定定理得结论(3)过点![]() 作
作![]() ,则根据面面垂直性质定理得
,则根据面面垂直性质定理得![]() 平面
平面![]() .即
.即![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角.最后通过解三角形得直线
所成的角.最后通过解三角形得直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
试题解析:(1)证明:如图,在三棱柱![]() 中,
中, ![]() ,且
,且![]() ,连接
,连接![]() ,在
,在![]() 中,因为
中,因为![]() 分别为
分别为![]() 的中点,
的中点,
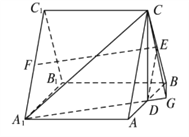
所以![]() 且
且![]() ,
,
又因为![]() 为
为![]() 的中点,可得
的中点,可得![]() ,且
,且![]() ,即四边形
,即四边形![]() 为平行四边形,所以
为平行四边形,所以![]() .
.
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)证明:由于底面![]() 是正三角形,
是正三角形, ![]() 为
为![]() 的中点,故
的中点,故![]() ,
,
又由于侧棱![]() 底面
底面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() ,因此
,因此![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(3)解:在平面![]() 内,过点
内,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]()
由于平面![]() 平面
平面![]() ,而直线
,而直线![]() 是平面
是平面![]() 与平面
与平面![]() 的交线,故
的交线,故![]() 平面
平面![]() .由此得
.由此得![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角.
所成的角.
设棱长为![]() ,可得
,可得![]() ,由
,由![]() ,易得
,易得![]() .
.
在![]() 中,
中, ![]() .所以直线
.所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点 在椭圆上.
在椭圆上.
(![]() )求椭圆
)求椭圆![]() 的方程.
的方程.
(![]() )设动直线
)设动直线![]() 与椭圆
与椭圆![]() 有且仅有一个公共点,判断是否存在以原点
有且仅有一个公共点,判断是否存在以原点![]() 为圆心的圆,满足此圆与
为圆心的圆,满足此圆与![]() 相交于两点
相交于两点![]() ,
, ![]() (两点均不在坐标轴上),且使得直线
(两点均不在坐标轴上),且使得直线![]() 、
、![]() 的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市小型机动车驾照“科二”考试中共有5项考查项目,分别记作①,②,③,④,⑤.
(1)某教练将所带10名学员“科二”模拟考试成绩进行统计(如表所示),并计算从恰有2项成绩不合格的学员中任意抽出2人进行补测(只测不合格的项目),求补测项目种类不超过3(![]() )项的概率.
)项的概率.
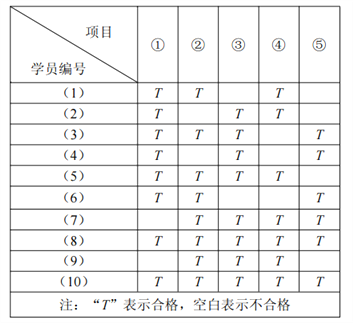
(2)“科二”考试中,学员需缴纳150元的报名费,并进行1轮测试(按①,②,③,④,⑤的顺序进行);如果某项目不合格,可免费再进行1轮补测;若第1轮补测中仍有不合格的项目,可选择“是否补考”;若补考则需缴纳300元补考费,并获得最多2轮补测机会,否则考试结束;每1轮补测都按①,②,③,④,⑤的顺序进行,学员在任何1轮测试或补测中5个项目均合格,方可通过“科二”考试,每人最多只能补考1次,某学院每轮测试或补考通过①,②,③,④,⑤各项测试的概率依次为![]() ,且他遇到“是否补考”的决断时会选择补考.
,且他遇到“是否补考”的决断时会选择补考.
①求该学员能通过“科二”考试的概率;
②求该学员缴纳的考试费用![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点![]() 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点![]() 的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为
的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为![]() 米,圆心角为
米,圆心角为![]() (弧度).
(弧度).
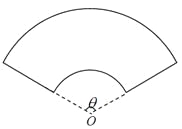
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 为何值时,
为何值时, ![]() 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的一系列对应值如下表:
的一系列对应值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据表格提供的数据求函数![]() 的一个解析式;
的一个解析式;
(2)根据(1)的结果,若函数![]() 周期为
周期为![]() ,当
,当![]() 时,方程
时,方程![]() 恰有两个不同的解,求实数
恰有两个不同的解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在用二次法求方程3x+3x-8=0在(1,2)内近似根的过程中,已经得到f(1)<0,f(1.5)>0,f(1.25)<0,则方程的根落在区间( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 不能确定
D. 不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com