
【题目】设点P是曲线 ![]() 上的任意一点,点P处的切线的倾斜角为α,则α的取值范围为 .
上的任意一点,点P处的切线的倾斜角为α,则α的取值范围为 .
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2﹣a2x+3.
(1)若a=2,求f(x)在[﹣1,2]上的最值;
(2)若f(x)在(﹣ ![]() ,1)上是减函数,求a的取值范围.
,1)上是减函数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的长轴长为
的长轴长为![]() ,且椭圆
,且椭圆![]() 与圆
与圆![]() :
: ![]() 的公共弦长为
的公共弦长为![]() .
.
(1)求椭圆![]() 的方程.
的方程.
(2)经过原点作直线![]() (不与坐标轴重合)交椭圆于
(不与坐标轴重合)交椭圆于![]() ,
, ![]() 两点,
两点, ![]() 轴于点
轴于点![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() ,求证:
,求证: ![]() ,
, ![]() ,
, ![]() 三点共线..
三点共线..
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 在平面直角坐标系
在平面直角坐标系![]() 下的参数方程为
下的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求曲线![]() 的普通方程及极坐标方程;
的普通方程及极坐标方程;
(2)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() :
: ![]() 与曲线
与曲线![]() 交于点
交于点![]() 与直线
与直线![]() 交于点
交于点![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() 以极点为平面直角坐标系的原点,极轴为
以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(Ⅰ)将曲线![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角
的倾斜角![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为R的函数f(x)满足f(x+2)=2f(x),当x∈[0,2)时,f(x)= 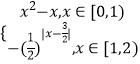 ,若x∈[﹣4,﹣2)时,f(x)≥
,若x∈[﹣4,﹣2)时,f(x)≥ ![]() 恒成立,则实数t的取值范围是( )
恒成立,则实数t的取值范围是( )
A.[﹣2,0)∪(0,1)
B.[﹣2,0)∪[1,+∞)
C.[﹣2,1]
D.(﹣∞,﹣2]∪(0,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(Ⅰ)当每辆车的月租金定为3600元时,能租出多少辆车?
(Ⅱ)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)= ![]() 是定义在(﹣1,1)上的奇函数,且f(
是定义在(﹣1,1)上的奇函数,且f( ![]() )=
)= ![]() .
.
(Ⅰ)求f(x)的解析式,
(Ⅱ)用函数单调性的定义证明f(x)在(﹣1,1)上是增函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+mx+n有两个零点﹣1与3.
(1)求出函数f(x)的解析式,并指出函数f(x)的单调递增区间;
(2)若g(x)=f(|x|)在x1 , x2∈[t,t+1]是增函数,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com