
观察下表:
1,
2,3,
4,5,6,7![]() ,
,
8,9,10,11,12,13,14,15,
……
问:(1)此表第n行的第一个数与最后一个数分别是多少?
(2)此表第n行的各个数之和是多少?
(3)2 012是第几行的第几个数?
(1)此表第n行的第1![]() 个数为2n-1,第n行共有2n-1个数,依次构成公差为1的等差数列.
个数为2n-1,第n行共有2n-1个数,依次构成公差为1的等差数列.
由等差数列的通项公式,此表第n行的最后一个数是2n-1+(2n-1-1)×1=2n-1;
(2)由等差数列的求和公式,此表第n行的各个数之和为![]() =22n-2+22n-3-2n-2,或2n-1×2n-1+
=22n-2+22n-3-2n-2,或2n-1×2n-1+![]() ×1=22n-2+22n-3-2n-2.
×1=22n-2+22n-3-2n-2.
(3)设2 012在此数表的第n行.
则2n-1≤2 012≤2n-1,n∈N+,可得n=11.
故2 012在此数表的第11行.
设2 012在此数表的第11行的第m个数,而第11行的第1个数为210,
因此,2 012是第11行的第989个数.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源:2013届福建泉州一中高二下学期期中考试文科数学试卷(解析版) 题型:填空题
观察下表:
1
2 3 4
3 4 5 6 7
4 5 6 7 8 9 10
......
则第______行的各数之和等于 .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南省四市九校高三上学期12月月考文科数学 题型:填空题
观察下表:
1
2 3 4
3 4 5 6 7
4 5 6 7 8 9 10
………………………………………………
则第
行的各数之和等于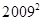
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省枣庄市高三上学期期末检测理科数学 题型:解答题
.(本题满分12分)
观察下表:
1,
2,3,
4,5,6,7,
8,9,10,11,12,13,14,15,
……
问:(1)此表第n行的第一个数与最后一个数分别是多少?
(2)此表第n行的各个数之和是多少?
(3)2012是第几行的第几个数?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com