
����Ŀ��ij������˾�¿���һ��ѧϰ��������������ѧ��֪ʶ���Ϊ�����ѹ�12�صĴ�����Ϸ��Ϊ�˼����������飬ÿ����һ�ض��������ɻ۱ң�һ����������ң����������ṩ�����ֽ�����������һ�֣�ÿ����һ�ؽ���40�۱ң��ڶ��֣�������һ�ؽ���4�۱ң��Ժ�ÿһ�ر�ǰһ�ضཱ��4�۱ң������֣�������һ�ؽ���0.5�۱ң��Ժ�ÿһ�ر�ǰһ�ؽ�����һ����������1��������Ϸ�涨�����������ڴ���ǰ��ѡһ�ֽ���������
�����贳��n �� n��N����n��12���غ����ֽ���������õĻ۱�����ΪAn �� Bn �� Cn �� �����An �� Bn �� Cn�ı���ʽ��
�����������һ�������ߣ�Ϊ�˵õ�����Ļ۱ң���Ӧ���ѡ����������
���𰸡��⣺���ߵ�һ�ֽ������������������û۱ҹ��ɳ����У��Ҹ����Ϊ40����An=40n��
�ڶ��ֽ���������������������û۱ҹ���������4������ҲΪ4�ĵȲ����У�
�� ![]() ��
��
�����ֽ������������������û۱ҹ���������0.5������Ϊ2�ĵȱ����У�
��  =
= ![]() ��
��
������An��Bn �� ��40n��2n2+2n�����n��19��
��n��N* �� ��n��12����An��Bn�������
��An��Cn �� �� ![]() �����n��10��
�����n��10��
�൱n��10ʱ��An���10��n��12ʱ��Cn��An ��
����������������һ�������ߣ������ܳ���Ĺ���С��10ʱ��Ӧ��ѡ�õ�һ�ֽ���������
�����ܳ���Ĺ������ڵ���10ʱ��Ӧ��ѡ�õ����ֽ�������
������������һ�ֽ������������������û۱ҹ��ɳ����У��Ҹ����Ϊ40���ɴ������An=40n���ڶ��ֽ���������������������û۱ҹ���������4������ҲΪ4�ĵȲ����У��ɴ������Bn�ı���ʽ�������ֽ������������������û۱ҹ���������0.5������Ϊ2�ĵȱ����У��ɴ������Cn�ı���ʽ��������An��Bn �� ��40n��2n2+2n�����n��19����n��12��֪An��Bn���������An��Cn �� �� ![]() �����n��10���ʵ�n��10ʱ��An���10��n��12ʱ��Cn��An �� �ɴ��ܹ�ѡ����ѵ�ѡ����������
�����n��10���ʵ�n��10ʱ��An���10��n��12ʱ��Cn��An �� �ɴ��ܹ�ѡ����ѵ�ѡ����������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������xOy�У�ֱ��l�IJ�������Ϊ{  ��tΪ����������OΪ���㣮x��������Ϊ����ļ�����ϵ�У�����C�ļ����귽��Ϊ��=4sin�ȩ�2cos�ȣ� ��I����ֱ��l����ͨ����������C��ֱ�����귽�̣�
��tΪ����������OΪ���㣮x��������Ϊ����ļ�����ϵ�У�����C�ļ����귽��Ϊ��=4sin�ȩ�2cos�ȣ� ��I����ֱ��l����ͨ����������C��ֱ�����귽�̣�
������ֱ��l��y��Ľ���ΪP��ֱ��l������C�Ľ���ΪA��B����|PA||PB|��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�a��b��c�ֱ�Ϊ�ڽ�A��B��C�ĶԱߣ����S= ![]() abcosC
abcosC
��1�����C�Ĵ�С��
��2���躯��f��x��= ![]() sin
sin ![]() cos
cos ![]() +cos2
+cos2 ![]() ����f��B�������ֵ����ȡ�����ֵʱ��B��ֵ��
����f��B�������ֵ����ȡ�����ֵʱ��B��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����{an}�ǹ���Ϊq�ĵȱ����У�
�������Ƶ�{an}��ǰn���ʽ��
���� ��q��1��֤������{an+1}���ǵȱ����У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
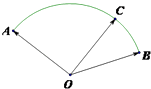
����Ŀ����ͼ���뾶Ϊ ![]() ������AOB��Բ�Ľ�Ϊ120�㣬��C��
������AOB��Բ�Ľ�Ϊ120�㣬��C�� ![]() �ϣ��ҡ�COB=30�㣬��
�ϣ��ҡ�COB=30�㣬�� ![]() �����+��=
�����+��= 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=��x3+1+a�� ![]() ��x��e��e����Ȼ�����ĵף���g��x��=3lnx��ͼ���ϴ��ڹ���x��ԳƵĵ㣬��ʵ��a��ȡֵ��Χ�ǣ� ��
��x��e��e����Ȼ�����ĵף���g��x��=3lnx��ͼ���ϴ��ڹ���x��ԳƵĵ㣬��ʵ��a��ȡֵ��Χ�ǣ� ��
A.[0��e3��4]
B.[0�� ![]() +2]
+2]
C.[ ![]() +2��e3��4]
+2��e3��4]
D.[e3��4��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A��B���ǡ�sinA��sinB�������ģ� ��
A.��ֱ�Ҫ����
B.��ֲ���Ҫ����
C.��Ҫ���������
D.�Ȳ����Ҳ����Ҫ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪{an}�ǵȲ����У�����a1=2��a4=14������{bn}����b1=1��b4=6����{an��bn}�ǵȱ����У� ����������{an}��{bn}��ͨ�ʽ��
������n��N* �� ����bn��bk��������������k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=xln��x��1����a��x��2���� ������a=2017��������f��x����x=2�������߷��̣�
��������x��2ʱ��f��x����0����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com