解:(1)当x∈(-1,0)时,-x∈(0,1),
有
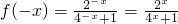
,
由f(x)为R上的奇函数,得f(-x)=-f(x),
∴当x∈(-1,0)时,
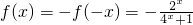
,(4分)
又f(0)=-f(0),f(0)=0,
∵f(-1)=-f(1),f(-1)=f(1-2)=f(1),
∴f(-1)=0,f(1)=0,(7分)
∴
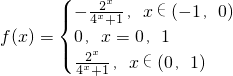
(8分)
(2)因为f(x+2)=f[(x+1)+1]=f(x+1-1)=f(x)
所以,2是函数f(x)的一个周期(2分)
∵f(x)是以2为周期的函数,即f(x-2k)=f(x),k∈Z,
设x∈[2k-1,2k+1],则x-2k∈[-1,1],
∴f(x-2k)=
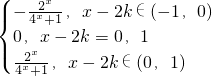
,(k∈Z)(6分)
f(x)在[2k-1,2k+1](k∈Z)上的解析式:
f(x)=
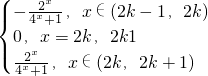
,(k∈Z).
(3)∵x∈(0,1)
设
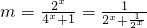
,(11分)
2
x∈(1,2),
∴
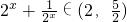
,
当x=0,1时,m=0,
即当x∈[0,1]时,
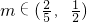
∪{0}. (14分)
∴当x∈[-1,1]时,|f(x)|∈
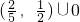
,
若关于x的方程|f(x)|=a无实数解,
则实数a的取值范围为:(-∞,0)∪(0,

)∪(

,+∞).
分析:(1)由定义域为R的奇函数f(x),又由当x∈(0,1)时,
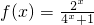
.利用奇函数f(-x)=-f(x),f(0)=0,我们可以求出f(x)在(-1,0)上的解析式,然后根据f(x)满足f(x)=f(x-2k)求出f(-1),f(1)的值,即得到f(x)在[-1,1]上的解析式;
(2)设x∈[2k-1,2k+1],则x-2k∈[-1,1],利用f(x)是以2为周期的函数,即f(x-2k)=f(x)可求解.
(3)根据当x∈(0,1)时,
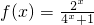
,求出函数在区间(0,1)上的值域,即可得到方程|f(x)|=a无实数解,时,a的取值范围.
点评:本题考查的知识点是函数与方程的综合运用,函数解析式的求法,函数的值域,其中(1)中易忽略对f(0),f(-1)及f(1)值的确定,而错解为
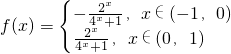
.

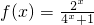 .
.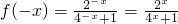 ,
,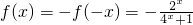 ,(4分)
,(4分)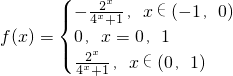 (8分)
(8分)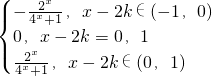 ,(k∈Z)(6分)
,(k∈Z)(6分)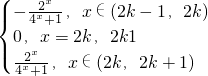 ,(k∈Z).
,(k∈Z).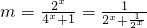 ,(11分)
,(11分)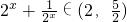 ,
,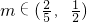 ∪{0}. (14分)
∪{0}. (14分)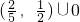 ,
, )∪(
)∪( ,+∞).
,+∞).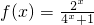 .利用奇函数f(-x)=-f(x),f(0)=0,我们可以求出f(x)在(-1,0)上的解析式,然后根据f(x)满足f(x)=f(x-2k)求出f(-1),f(1)的值,即得到f(x)在[-1,1]上的解析式;
.利用奇函数f(-x)=-f(x),f(0)=0,我们可以求出f(x)在(-1,0)上的解析式,然后根据f(x)满足f(x)=f(x-2k)求出f(-1),f(1)的值,即得到f(x)在[-1,1]上的解析式;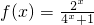 ,求出函数在区间(0,1)上的值域,即可得到方程|f(x)|=a无实数解,时,a的取值范围.
,求出函数在区间(0,1)上的值域,即可得到方程|f(x)|=a无实数解,时,a的取值范围.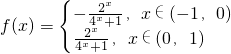 .
. 

 考前必练系列答案
考前必练系列答案