
【题目】某生态公园的平面图呈长方形(如图),已知生态公园的长AB=8(km),宽AD=4(km),M,N分别为长方形ABCD边AD,DC的中点,P,Q为长方形ABCD边AB,BC(不含端点)上的一点.现公园管理处拟修建观光车道P﹣Q﹣N﹣M﹣P,要求观光车道围成四边形(如图阴影部分)的面积为15(km2),设BP=x(km),BQ=y(km), 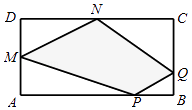
(1)试写出y关于x的函数关系式,并求出x的取值范围;
(2)若B为公园入口,P,Q为观光车站,观光车站P位于线段AB靠近入口B的一侧.经测算,每天由B入口至观光车站P,Q乘坐观光车的游客数量相等,均为1万人,问如何确定观光车站P,Q的位置,使所有游客步行距离之和最大,并求出最大值.
【答案】
(1)解:∵M,N是AD,CD的中点,AB=8,AD=4,BP=x,BQ=y,
∴S△AMP= ![]() =8﹣x,S△DMN=
=8﹣x,S△DMN= ![]() =4,S△NCQ=
=4,S△NCQ= ![]() =8﹣2y,S△BPQ=
=8﹣2y,S△BPQ= ![]() ,
,
∵观光车道围成四边形(如图阴影部分)的面积为15(km2),
∴8﹣x+4+8﹣2y+ ![]() xy=4×8﹣15=17,
xy=4×8﹣15=17,
∴y= 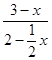 =
= ![]() .
.
令0<y<4,即0< ![]() <4,解得0<x<3或5<x<8.
<4,解得0<x<3或5<x<8.
(2)解:由题意可知0<x<3,
∴x+y=x+ ![]() =x+2﹣
=x+2﹣ ![]() ,
,
令f(x)=x+2﹣ ![]() ,则f′(x)=1﹣
,则f′(x)=1﹣ ![]() ,
,
令f′(x)=0得x=4﹣ ![]() ,
,
∴当0<x ![]() 时.f′(x)>0,当4﹣
时.f′(x)>0,当4﹣ ![]() <x<3时,f′(x)<0,
<x<3时,f′(x)<0,
∴f(x)在(0,4﹣ ![]() )上单调递增,在(4﹣
)上单调递增,在(4﹣ ![]() ,3)上单调递减,
,3)上单调递减,
∴当x=4﹣ ![]() 时,f(x)取得最大值6﹣2
时,f(x)取得最大值6﹣2 ![]() .
.
∴所有游客的步行距离之和的最大值为20000×(6﹣2 ![]() )=40000(3﹣
)=40000(3﹣ ![]() )km.
)km.
【解析】(1)根据面积列方程得出y关于x的解析式;(2)利用导数求出x+y的最大值,从而得出步行距离之和的最大值.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且满足(2b﹣c)cosA﹣acosC=0.
(1)求角A的大小;
(2)若a=4,求△ABC周长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(2cosx,
=(2cosx, ![]() sinx),
sinx), ![]() =(3cosx,﹣2cosx),设函数f(x)=
=(3cosx,﹣2cosx),设函数f(x)= ![]()
![]()
(1)求f(x)的最小正周期;
(2)若x∈[0, ![]() ],求f(x)的值域.
],求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|x﹣a|+2x(a∈R)
(1)当a=4时,解不等式f(x)≥8;
(2)当a∈[0,4]时,求f(x)在区间[3,4]上的最小值;
(3)若存在a∈[0,4],使得关于x的方程f(x)=tf(a)有3个不相等的实数根,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三角形的顶点分别为A(﹣1,3),B(3,2),C(1,0)
(1)求BC边上高的长度;
(2)若直线l过点C,且在l上不存在到A,B两点的距离相等的点,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的公比q>1,a1=1,且a1 , a3 , a2+14成等差数列,数列{bn}满足a1b1+a2b2+…+anbn=(n﹣1)3n+1(n∈N*).
(1)求数列{an}和{bn}的通项公式;
(2)令cn=(﹣1)n ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com