
【题目】在极坐标系中,已知三点O(0,0),A(2, ![]() ),B(2
),B(2 ![]() ,
, ![]() ).
).
(1)求经过O,A,B的圆C1的极坐标方程;
(2)以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,圆C2的参数方程为 ![]() (θ是参数),若圆C1与圆C2外切,求实数a的值.
(θ是参数),若圆C1与圆C2外切,求实数a的值.
【答案】
(1)解:将O,A,B三点化成普通坐标为O(0,0),A(0,2),B(2,2).
∴圆C1的圆心为(1,1),半径为 ![]() ,
,
∴圆C1的普通方程为(x﹣1)2+(y﹣1)2=2,
将 ![]() 代入普通方程得ρ2﹣2ρcosθ﹣2ρsinθ=0,
代入普通方程得ρ2﹣2ρcosθ﹣2ρsinθ=0,
∴ρ=2 ![]() sin(
sin( ![]() ).
).
(2)解:∵圆C2的参数方程为 ![]() (θ是参数),
(θ是参数),
∴圆C2的普通方程为(x+1)2+(y+1)2=a2.∴圆C2的圆心为(﹣1,﹣1),半径为|a|,
∵圆C1与圆C2外切,∴2 ![]() =
= ![]() +|a|,解得a=±
+|a|,解得a=± ![]() .
.
【解析】(1)求出圆C1的普通方程,再将普通方程转化为极坐标方程;(2)将圆C2化成普通方程,根据两圆外切列出方程解出a.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣1|+|ax﹣5|(0<a<5).
(1)当a=1时,求不等式f(x)≥9的解集;
(2)如果函数y=f(x)的最小值为4,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n(n∈N*)项和为Sn , a3=3,且λSn=anan+1 , 在等比数列{bn}中,b1=2λ,b3=a15+1. (Ⅰ)求数列{an}及{bn}的通项公式;
(Ⅱ)设数列{cn}的前n(n∈N*)项和为Tn , 且 ![]() ,求Tn .
,求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为1的正方体ABCD﹣A1B1C1D1中,AC∩BD=O,E是线段B1C(含端点)上的一动点,则 ①OE⊥BD1;
②OE∥面A1C1D;
③三棱锥A1﹣BDE的体积为定值;
④OE与A1C1所成的最大角为90°.
上述命题中正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学家赵爽设计的弦图(如图1)是由四个全等的直角三角形拼成,四个全等的直角三角形也可拼成图2所示的菱形,已知弦图中,大正方形的面积为100,小正方形的面积为4,则图2中菱形的一个锐角的正弦值为( ) 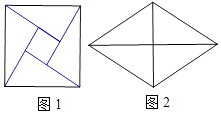
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先将函数y=2sinx的图象纵坐标不变,横坐标压缩为原来一半,再将得到的图象向左平移 ![]() 个单位,则所得图象的对称轴可以为( )
个单位,则所得图象的对称轴可以为( )
A.x=﹣ ![]()
B.x= ![]()
C.x=﹣ ![]()
D.x= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=plnx+(p﹣1)x2+1.
(1)讨论函数f(x)的单调性;
(2)当P=1时,f(x)≤kx恒成立,求实数k的取值范围;
(3)证明:1n(n+1)<1+ ![]() …+
…+ ![]() (n∈N+).
(n∈N+).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com