
【题目】已知函数![]()
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求函数的极值;
垂直,求函数的极值;
(2)设函数![]() .当
.当![]() =
=![]() 时,若区间[1,e]上存在x0,使得
时,若区间[1,e]上存在x0,使得![]() ,求实数
,求实数![]() 的取值范围.(
的取值范围.(![]() 为自然对数底数)
为自然对数底数)
【答案】(1)极小值为![]() ;(2)
;(2)
【解析】试题分析:(1)求出函数的导数,计算![]() 的值,求出
的值,求出![]() ,从而求出
,从而求出![]() 的单调区间,求出函数的极值即可;(2)令
的单调区间,求出函数的极值即可;(2)令![]() ,根据函数的单调性求出
,根据函数的单调性求出![]() 的最小值,从而求出
的最小值,从而求出![]() 的范围即可.
的范围即可.
试题解析:(1)![]() (
(![]() ),因为曲线
),因为曲线![]() 在点(1,f(1))处的切线与直线
在点(1,f(1))处的切线与直线![]() 垂直,所以
垂直,所以![]() ,即
,即![]() ,解得
,解得![]() .所以
.所以![]() , ∴当
, ∴当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递减;当
上单调递减;当![]() 时,
时, ![]() ,f(x)在(2,+∞)上单调递增;∴当x=2时,f(x)取得极小值
,f(x)在(2,+∞)上单调递增;∴当x=2时,f(x)取得极小值![]() ,∴f(x)极小值为ln2.
,∴f(x)极小值为ln2.
(2)令![]() ,则
,则![]() ,欲使在区间上
,欲使在区间上![]() 上存在
上存在![]() ,使得
,使得![]() ,只需在区间
,只需在区间![]() 上
上![]() 的最小值小于零.令
的最小值小于零.令![]() 得,
得, ![]() 或
或![]() .当
.当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递减,则
上单调递减,则![]() 的最小值为
的最小值为![]() ,∴
,∴![]() ,解得
,解得![]() ,∵
,∵![]() ,∴
,∴![]() ;当
;当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递增,则
上单调递增,则![]() 的最小值为
的最小值为![]() ,∴
,∴![]() ,解得
,解得![]() ,∴
,∴![]() ;当
;当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,则
上单调递增,则![]() 的最小值为
的最小值为![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() ,此时
,此时![]() 不成立.综上所述,实数m的取值范围为
不成立.综上所述,实数m的取值范围为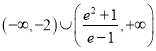


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:
【题目】下列事件A,B是独立事件的是( )
A. 一枚硬币掷两次,A=“第一次为正面向上”,B=“第二次为反面向上”
B. 袋中有两个白球和两个黑球,不放回地摸两球,A=“第一次摸到白球”,B=“第二次摸到白球”
C. 掷一枚骰子,A=“出现点数为奇数”,B=“出现点数为偶数”
D. A=“人能活到20岁”,B=“人能活到50岁”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,已知曲线
轴正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若两条互相垂直的直线都经过原点(两条直线与坐标轴都不重合)且与曲线![]() 分别交于点
分别交于点![]() (异于原点),且
(异于原点),且![]() ,求这两条直线的直角坐标方程.
,求这两条直线的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知直线l过点P(2,2).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ﹣ρcos2θ﹣4cosθ=0.
(1)求C的直角坐标方程;
(2)若l与C交于A,B两点,求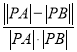 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 前
前![]() 项和为
项和为![]() ,对任意
,对任意![]() ,点
,点![]() 都在函数
都在函数![]() 图像上.
图像上.
(1)求![]() 、
、![]() 、
、![]() ,并猜想数列
,并猜想数列![]() 的通项公式;
的通项公式;
(2)用数学归纳法证明(1)的猜想;
(3)若数列![]() 满足:
满足:![]() ,
,![]() ,且对任意的
,且对任意的![]() ,都有
,都有![]() 、
、![]() 、
、![]() 成公比为
成公比为![]() 的等比数列,
的等比数列,![]() 、
、![]() 、
、![]() 成等差数列,设
成等差数列,设![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图231所示.
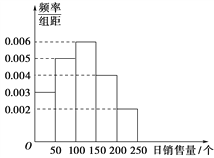 图231
图231
将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
(1)求在未来连续3天里,有连续2天的日销售量都不低于100个且另1天的日销售量低于50个的概率;
(2)用X表示在未来3天里日销售量不低于100个的天数,求随机变量X的分布列,期望E(X)及方差D(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4—4,坐标系与参数方程
已知曲线![]() ,直线
,直线![]() :
:![]() (
(![]() 为参数).
为参数).
(I)写出曲线![]() 的参数方程,直线
的参数方程,直线![]() 的普通方程;
的普通方程;
(II)过曲线![]() 上任意一点
上任意一点![]() 作与
作与![]() 夹角为
夹角为![]() 的直线,交
的直线,交![]() 于点
于点![]() ,
,![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com