考点:平面向量的基本定理及其意义,平面向量数量积的运算
专题:平面向量及应用
分析:(1)根据向量的坐标运算可以求出m,n,然后带入m
2+n
2即可.
(2)先假设O是△ABC的重心,因为AB的中点在x轴上,所以AB边的中线在x轴上,所以可以求出C(-
,0).这时可以求出线段BC的中点坐标,可以验证BC边的中点不在直线OA上,所以O不是△AB的重心.C
解答:
解:(1)根据条件得:
m(1,1)+n(1,-1)=2(cosθ,sinθ);
∴
;
∴
| | m=(sinθ+cosθ) | | n=(cosθ-sinθ) |
| |
;
∴m
2+n
2=2(1+sin2θ)+2(1-sin2θ)=4.
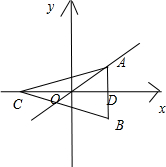
(2)原点O不能成为△ABC的重心.如下图:由A,B点的坐标得线段AB的中点D(1,0),若O是△ABC的重心,OD便在线段AB的中线上,所以C在OD上,即C在x轴上;
∴
sinθ=0;
∴
cosθ=-,∴C(
-,0);
∴线段BC的中点坐标为:(
,-).
AO是BC边上的中线,并且直线AO的方程为:y=x;
显然,线段BC的中点不在直线AO上;
∴所以O不是△ABC的重心.
点评:本题考查向量的坐标运算,重心的概念,二倍角的正弦公式,sin2α+cos2α=1.

 解:(1)根据条件得:
解:(1)根据条件得:

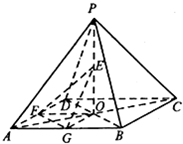 如图,四棱锥P-ABCD的底面为正方形,AC∩BD=O,PO⊥平面ABCD,E、F、G分别是PO、AD、AB的中点.
如图,四棱锥P-ABCD的底面为正方形,AC∩BD=O,PO⊥平面ABCD,E、F、G分别是PO、AD、AB的中点. 如图,已知平行四边形ABCD和平行四边形ACEF所在的平面相交于直线AC,EC⊥平面ABCD,AB=1,AD=2,∠ADC=60°,AF=
如图,已知平行四边形ABCD和平行四边形ACEF所在的平面相交于直线AC,EC⊥平面ABCD,AB=1,AD=2,∠ADC=60°,AF=