[题目]已知函数f(x)为奇函数.且当x＞0时.f(x)=x2+ .则f(﹣1)=( )A.2B.1C.0D.﹣2 题目和参考答案——青夏教育精英家教网—

【题目】已知函数f（x）为奇函数，且当x＞0时，f（x）=x2+ ，则f（﹣1）=（）
A.2
B.1
C.0
D.﹣2

【答案】D
【解析】解：∵已知函数f（x）为奇函数，且当x＞0时，f（x）=x2+ ，则f（﹣1）=﹣f（1）=﹣（1+1）=﹣2，故选D．
【考点精析】利用函数奇偶性的性质和函数的值对题目进行判断即可得到答案，需要熟知在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇；函数值的求法：①配方法(二次或四次)；②“判别式法”；③反函数法；④换元法；⑤不等式法；⑥函数的单调性法．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，在四棱锥P﹣ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，E是PC的中点．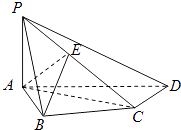

（1）证明CD⊥AE；
（2）证明PD⊥平面ABE；

（3）求二面角A﹣PD﹣C的正切值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知定义在[﹣2，2]上的函数y=f（x）和y=g（x），其图象如图所示：给出下列四个命题：
①方程f[g（x）]=0有且仅有6个根 ②方程g[f（x）]=0有且仅有3个根
③方程f[f（x）]=0有且仅有5个根 ④方程g[g（x）]=0有且仅有4个根
其中正确命题的序号（）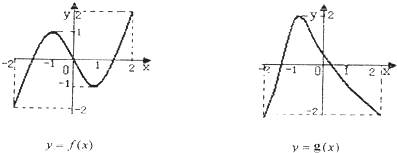

A.①②③
B.②③④
C.①②④
D.①③④

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】过双曲线 =1（a＞0，b＞0）的左焦点F（﹣c，0）作圆x2+y2=a2的切线，切点为E，延长FE交抛物线y2=4cx于点P，O为坐标原点，若 = （ + ），则双曲线的离心率为（）
A.
B.
C.
D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，三棱柱ABC﹣A1B1C1的底面是边长为2的正三角形且侧棱垂直于底面，侧棱长是，D是AC的中点．
（1）求证：B1C∥平面A1BD；
（2）求二面角A1﹣BD﹣A的大小；
（3）求直线AB1与平面A1BD所成的角的正弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=ax+lnx（a∈R）．（Ⅰ）若a=2，求曲线y=f（x）在x=1处切线的斜率；
（Ⅱ）求f（x）的单调区间；
（Ⅲ）设g（x）=x2﹣2x+2，若对任意x1∈（0，+∞），均存在x2∈[0，1]，使得f（x1）＜g（x2），求a的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=ln（ax+1）+ ﹣x2﹣ax（a∈R）
（1）若y=f（x）在[4，+∞）上为增函数，求实数a的取值范围；
（2）当a≥ 时，设g（x）=ln[x2（ax+1）]+ ﹣3ax﹣f（x）（x＞0）的两个极值点x1 ， x2（x1＜x2）恰为φ（x）=lnx﹣cx2﹣bx的零点，求y=（x1﹣x2）φ′（）的最小值．