
【题目】已知偶函数![]() 满足
满足![]() ,且当
,且当![]() 时,
时,![]() ,关于
,关于![]() 的不等式
的不等式![]() 在
在![]() 上有且只有
上有且只有![]() 个整数解,则实数
个整数解,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】C
【解析】
推导出函数![]() 是以
是以![]() 为周期的周期函数,利用导数分析函数
为周期的周期函数,利用导数分析函数![]() 的单调性与极值,可作出函数
的单调性与极值,可作出函数![]() 在区间
在区间![]() 上的图象,由题意可知,不等式
上的图象,由题意可知,不等式![]() 在
在![]() 上有且只有
上有且只有![]() 个整数解,然后分
个整数解,然后分![]() 、
、![]() 、
、![]() 三种情况讨论,数形结合可求得实数
三种情况讨论,数形结合可求得实数![]() 的取值范围.
的取值范围.
由于函数![]() 为偶函数,则
为偶函数,则![]() ,即
,即![]() ,
,
所以,函数![]() 是以
是以![]() 为周期的周期函数,
为周期的周期函数,
当![]() 时,
时,![]() ,
,![]() ,令
,令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减.
单调递减.
所以,![]() ,又
,又![]() ,
,
作出函数![]() 在
在![]() 上的图象如下图所示:
上的图象如下图所示:
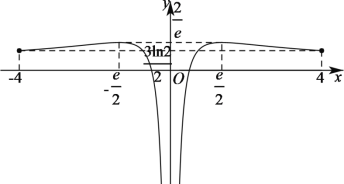
由于关于![]() 的不等式
的不等式![]() 在
在![]() 上有且只有
上有且只有![]() 个整数解,
个整数解,
则关于![]() 的不等式
的不等式![]() 在
在![]() 上有且只有
上有且只有![]() 个整数解.
个整数解.
①若![]() ,由
,由![]() 可得
可得![]() ,
,
此时,该不等式在![]() 有
有![]() 个整数解,不合乎题意;
个整数解,不合乎题意;
②若![]() ,由
,由![]() 可得
可得![]() 或
或![]() .
.
不等式![]() 在
在![]() 上无整数解;
上无整数解;
不等式![]() 在
在![]() 上有
上有![]() 个整数解.不合乎题意;
个整数解.不合乎题意;
③若![]() ,由
,由![]() 可得
可得![]() 或
或![]() .
.
不等式![]() 在
在![]() 上无整数解,则不等式
上无整数解,则不等式![]() 在
在![]() 上有
上有![]() 个整数解,
个整数解,
由于![]() ,且
,且![]() ,
,![]() ,
,
所以,![]() ,即
,即![]() ,解得
,解得![]() .
.
因此,实数![]() 的取值范围是
的取值范围是![]() .
.
故选:C.


科目:高中数学 来源: 题型:
【题目】某媒体对“男女延迟退休”这一公众关注的问题进行了民意调查,下表是在某单位调查后得到的数据(人数):
赞同 | 反对 | 合计 | |
男 | 5 | 6 | 11 |
女 | 11 | 3 | 14 |
合计 | 16 | 9 | 25 |
(1)能否有90%以上的把握认为对这一问题的看法与性别有关?
(2)进一步调查:
①从赞同“男女延迟退休”的![]() 人中选出
人中选出![]() 人进行陈述发言,求事件“男士和女士各至少有
人进行陈述发言,求事件“男士和女士各至少有![]() 人发言”的概率;
人发言”的概率;
②从反对“男女延迟退休”的![]() 人中选出
人中选出![]() 人进行座谈,设选出的
人进行座谈,设选出的![]() 人中女士人数为
人中女士人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
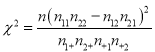
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按![]() 元/度收费,超过200度但不超过400度的部分按
元/度收费,超过200度但不超过400度的部分按![]() 元/度收费,超过400度的部分按1.0元/度收费.
元/度收费,超过400度的部分按1.0元/度收费.

(Ⅰ)求某户居民用电费用![]() (单位:元)关于月用电量
(单位:元)关于月用电量![]() (单位:度)的函数解析式;
(单位:度)的函数解析式;
(Ⅱ)为了了解居民的用电情况,通过抽样,获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年1月份用电费用不超过260元的占![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(Ⅲ)在满足(Ⅱ)的条件下,若以这100户居民用电量的频率代替该月全市居民用户用电量的概率,且同组中的数据用该组区间的中点代替,记![]() 为该居民用户1月份的用电费用,求
为该居民用户1月份的用电费用,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地![]() 规划建成一个矩形的高科技工业园区.已知
规划建成一个矩形的高科技工业园区.已知![]() ,
,![]() ,
,![]() ,曲线段
,曲线段![]() 是以点
是以点![]() 为顶点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落在
为顶点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落在![]() 、
、![]() 上,且一个顶点
上,且一个顶点![]() 落在曲线段
落在曲线段![]() 上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到
上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到![]() ).
).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只苍蝇和![]() 只蜘蛛被放置在
只蜘蛛被放置在![]() 方格表的一些交点处.一次操作包括以下步骤:首先,苍蝇移动到相邻的交点处或者原地不动,然后,每只蜘蛛移动到相邻交点处或者原地不动(同一交点可以同时停留多只蜘蛛).假设每只蜘蛛和苍蝇总是知道其他蜘蛛和苍蝇的位置.
方格表的一些交点处.一次操作包括以下步骤:首先,苍蝇移动到相邻的交点处或者原地不动,然后,每只蜘蛛移动到相邻交点处或者原地不动(同一交点可以同时停留多只蜘蛛).假设每只蜘蛛和苍蝇总是知道其他蜘蛛和苍蝇的位置.
(1)找出最小的正整数![]() ,使得在有限次操作内,蜘蛛能够抓住苍蝇,且与其初始位置无关;
,使得在有限次操作内,蜘蛛能够抓住苍蝇,且与其初始位置无关;
(2)在![]() 的空间三维方格中,(1)中的结论又是怎样?
的空间三维方格中,(1)中的结论又是怎样?
(注)题中相邻是指一个交点仅有一个坐标与另一个交点的同一坐标不同,且差值为1;题中抓住是指蜘蛛和苍蝇位于同一交点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]()
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)①证明:当![]() 时,函数
时,函数![]() 在
在![]() 上恰有一个极值点
上恰有一个极值点![]() ;
;
②求实数![]() 的取值范围,使得对任意的
的取值范围,使得对任意的![]() ,恒有
,恒有![]() 成立.
成立.
注:![]() 为自然对数的底数.
为自然对数的底数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某大型活动中,甲、乙等五名志愿者被随机地分到A,B,C,D四个不同的岗位服务,每个岗位至少有一名志愿者.
(1)求甲、乙两人同时参加A岗位服务的概率;
(2)求甲、乙两人不在同一个岗位服务的概率;
(3)求五名志愿者中仅有一人参加A岗位服务的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,底面
,底面![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 中点,点
中点,点![]() 在线段
在线段![]() 上.
上.
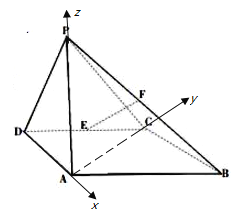
(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]()
![]()
![]()
![]() ,求实数
,求实数![]() 使直线
使直线![]() 与平面
与平面![]() 所成角和直线
所成角和直线![]() 与平面
与平面![]() 所成角相等.
所成角相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:
满足:![]() ,当
,当![]() ,
,![]() 时.
时.
![]() 其中
其中![]() 表示
表示![]() ,
,![]() ,
,![]() ,
,![]() 中的最大项
中的最大项![]() ,有以下结论:
,有以下结论:
![]() 若数列
若数列![]() 是常数列,则
是常数列,则![]()
![]() 若数列
若数列![]() 是公差
是公差![]() 的等差数列,则
的等差数列,则![]() ;
;
![]() 若数列
若数列![]() 是公比为q的等比数列,则
是公比为q的等比数列,则![]()
则其中正确的结论是______![]() 写出所有正确结论的序号
写出所有正确结论的序号![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com