
【题目】已知数列{an}的前n项和为Sn , an>0,且满足:(an+2)2=4Sn+4n+1,n∈N* .
(1)求a1及通项公式an;
(2)若bn=(﹣1)nan , 求数列{bn}的前n项和Tn .
【答案】
(1)解:∵(an+2)2=4Sn+4n+1,n∈N*,∴ ![]() =4a1+5,a1>0,解得a1=1.
=4a1+5,a1>0,解得a1=1.
n≥2时, ![]() =4Sn﹣1+4(n﹣1)+1,相减可得:
=4Sn﹣1+4(n﹣1)+1,相减可得: ![]() =0,an>0,化为:an﹣an﹣1=2.
=0,an>0,化为:an﹣an﹣1=2.
∴数列{an}是等差数列,公差为2,首项为1.
∴an=1+2(n﹣1)=2n﹣1
(2)解:bn=(﹣1)nan=(﹣1)n(2n﹣1).
n=2k(k∈N*)时,b2k﹣1+b2k=﹣(2n﹣1)+(2n+1)=2.
∴数列{bn}的前n项和Tn=n.
n=2k﹣1(k∈N*)时,b2k+b2k+1=(2n﹣1)﹣(2n+1)=﹣2.
∴数列{bn}的前n项和Tn=﹣1﹣ ![]() =﹣n.
=﹣n.
∴Tn= ![]() ,k∈N*
,k∈N*
【解析】(1)利用数列递推关系、等差数列的通项公式即可得出.(2)对n分类讨论,利用分组求和即可得出.
【考点精析】根据题目的已知条件,利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系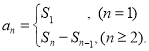 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在平面斜坐标系xOy中,∠xOy=60°,平面上任意一点P关于斜坐标系的斜坐标是这样定义的:若![]() =xe1+ye2(其中e1,e2分别为x轴、y轴同方向的单位向量),则点P的斜坐标为(x,y).
=xe1+ye2(其中e1,e2分别为x轴、y轴同方向的单位向量),则点P的斜坐标为(x,y).
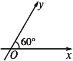
(1)若点P在斜坐标系xOy中的斜坐标为(2,-2),求点P到原点O的距离.
(2)求以原点O为圆心,1为半径的圆在斜坐标系xOy中的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下是新兵训练时,某炮兵连8周中炮弹对同一目标的命中情况的柱状图: 
(1)计算该炮兵连这8周中总的命中频率p0 , 并确定第几周的命中频率最高;
(2)以(1)中的p0作为该炮兵连炮兵甲对同一目标的命中率,若每次发射相互独立,且炮兵甲发射3次,记命中的次数为X,求X的数学期望;
(3)以(1)中的p0作为该炮兵连炮兵对同一目标的命中率,试问至少要用多少枚这样的炮弹同时对该目标发射一次,才能使目标被击中的概率超过0.99?(取lg0.4=﹣0.398)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,焦点
的中心在原点,焦点![]() 、
、![]() 在
在![]() 轴上,离心率为
轴上,离心率为![]() ,在椭圆
,在椭圆![]() 上有一动点
上有一动点![]() 与
与![]() 、
、![]() 的距离之和为4,
的距离之和为4,
(Ⅰ) 求椭圆E的方程;
(Ⅱ) 过![]() 、
、![]() 作一个平行四边形,使顶点
作一个平行四边形,使顶点![]() 、
、![]() 、
、![]() 、
、![]() 都在椭圆
都在椭圆![]() 上,如图所示.判断四边形
上,如图所示.判断四边形![]() 能否为菱形,并说明理由.
能否为菱形,并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车给市民出行带来了诸多便利,某公司购买了一批单车投放到某地给市民使用,
据市场分析,每辆单车的营运累计利润y(单位:元)与营运天数x![]() 满足函数关系
满足函数关系
式![]() .
.
(1)要使营运累计利润高于800元,求营运天数的取值范围;
(2)每辆单车营运多少天时,才能使每天的平均营运利润![]() 的值最大?
的值最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有甲、乙两个研发小组,他们研究新产品成功的概率分别为 ![]() 和
和 ![]() ,现安排甲组研发新产品A,乙组研发新产品B,设甲、乙两组的研发相互独立.
,现安排甲组研发新产品A,乙组研发新产品B,设甲、乙两组的研发相互独立.
(1)求恰好有一种新产品研发成功的概率;
(2)若新产品A研发成功,预计企业可获得利润120万元,不成功则会亏损50万元;若新产品B研发成功,企业可获得利润100万元,不成功则会亏损40万元,求该企业获利ξ万元的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,已知CA=1,CB=2,∠ACB=60°.

(1)求|![]() |;
|;
(2)已知点D是AB上一点,满足![]() =λ
=λ![]() ,点E是边CB上一点,满足
,点E是边CB上一点,满足![]() =λ
=λ![]() .
.
①当λ=![]() 时,求
时,求![]()
![]() ;
;
②是否存在非零实数λ,使得![]() ⊥
⊥![]() ?若存在,求出的λ值;若不存在,请说明理由.
?若存在,求出的λ值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,离心率为
的中心在原点,离心率为![]() ,右焦点到直线
,右焦点到直线![]() 的距离为2.
的距离为2.
(1)求椭圆![]() 的方程;
的方程;
(2)椭圆下顶点为![]() ,直线
,直线![]() (
(![]() )与椭圆相交于不同的两点
)与椭圆相交于不同的两点![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com