2 {x|-7<x<5}
分析:①曲线
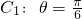
(ρ∈R)是过极点倾斜角为

的射线,所在直线的方程是y=

x,曲线
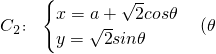
为参数,a为常数,a>0)是圆心为(a,0),半径为

的圆,由|AB|=2,得
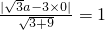
,由此能求出a.
②因为已知a、b、c是实数,且a
2+2b
2+3c
2=6根据柯西不等式得到|a+2b+3c|≤6,a+2b+3c的最大值为6,a+2b+3c的最小值为-6.所以使得不等式a+2b+3c>|x+1|成立的条件是|x+1|<6,由此能求出x的范围.
解答:①∵曲线
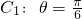
(ρ∈R)是过极点(0,0)且倾斜角为

的直线,
∴曲线C
1所在直线的方程是y=

x,
∵曲线
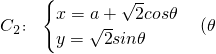
为参数,a为常数,a>0)是圆心为(a,0),半径为

的圆,
∴由|AB|=2,得圆心(a,0)到曲线C
1y=

x的距离d=
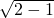
=1,
由点到直线的距离公式,得
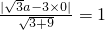
,
解得a=±2.
∵a>0,
∴a=2.
故答案为:2.
②因为已知a、b、c是实数,且a
2+2b
2+3c
2=6
根据柯西不等式(a
2+b
2+c
2)(x
2+y
2+z
2)≥(ax+by+cz)
2故有(a
2+2b
2+3c
2)(1
2+
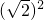
+(

)
2)≥(a+2b+3c)
2故(a+2b+3c)
2≤36,即|a+2b+3c|≤6,
即a+2b+3c的最大值为6,a+2b+3c的最小值为-6;
∴使得不等式a+2b+3c>|x+1|成立的条件是|x+1|<6,
解得{x|-7<x<5}.
故答案为:{x|-7<x<5}.
点评:第①题考查简单曲线的极坐标方程,是基础题.解题时要认真审题,注意点到直线 的距离公式的灵活运用.
第②题考查一般形式的柯西不等式的应用,解题时要认真审题,注意含绝对值不等式的解法.

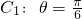 (ρ∈R)与曲线
(ρ∈R)与曲线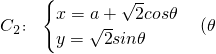 为参数,a为常数,a>0)有两个交点A、B,且|AB|=2,则实数a的值为________.
为参数,a为常数,a>0)有两个交点A、B,且|AB|=2,则实数a的值为________.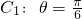 (ρ∈R)是过极点倾斜角为
(ρ∈R)是过极点倾斜角为 的射线,所在直线的方程是y=
的射线,所在直线的方程是y= x,曲线
x,曲线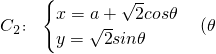 为参数,a为常数,a>0)是圆心为(a,0),半径为
为参数,a为常数,a>0)是圆心为(a,0),半径为 的圆,由|AB|=2,得
的圆,由|AB|=2,得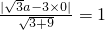 ,由此能求出a.
,由此能求出a.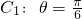 (ρ∈R)是过极点(0,0)且倾斜角为
(ρ∈R)是过极点(0,0)且倾斜角为 的直线,
的直线, x,
x,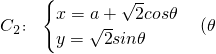 为参数,a为常数,a>0)是圆心为(a,0),半径为
为参数,a为常数,a>0)是圆心为(a,0),半径为 的圆,
的圆, x的距离d=
x的距离d=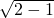 =1,
=1,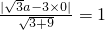 ,
, +(
+(  )2)≥(a+2b+3c)2
)2)≥(a+2b+3c)2

 (2012•黄冈模拟)(选做题:请在下列两题中任选一题作答,如果多做,则按所做的第一题评分)
(2012•黄冈模拟)(选做题:请在下列两题中任选一题作答,如果多做,则按所做的第一题评分)