
已知数列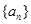 满足:
满足: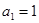 ,
,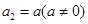 ,
,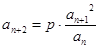 (其中
(其中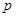 为非零常数,
为非零常数,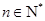 ).
).
(1)判断数列 是不是等比数列?
是不是等比数列?
(2)求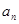 ;
;
(3)当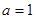 时,令
时,令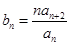 ,
,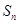 为数列
为数列 的前
的前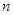 项和,求
项和,求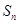 .
.
(1)由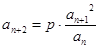 ,得
,得 .
. .
.  (非零常数),
(非零常数),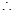 数列
数列 是等比数列.
是等比数列.
(2)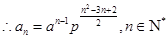 .
.
(3)
解析试题分析:(1)由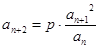 ,得
,得 . 1分
. 1分
令 ,则
,则 ,
, .
.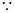
 ,
, ,
, (非零常数),
(非零常数),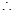 数列
数列 是等比数列. 3分
是等比数列. 3分
(2)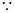 数列
数列 是首项为
是首项为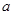 ,公比为
,公比为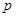 的等比数列,
的等比数列, 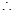
 ,即
,即 . 4分
. 4分
当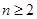 时,
时,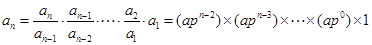
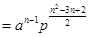 , 6分
, 6分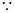
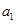 满足上式,
满足上式, 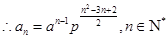 . 7分
. 7分
(3) ,
,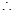 当
当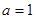 时,
时,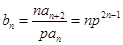 . 8分
. 8分 , ①
, ① ②
②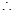 当
当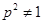 ,即
,即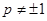 时,①
时,① ②得:
②得: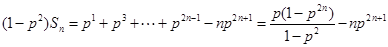 ,
,
即 . 11分
. 11分
而当 时,
时, , 12分
, 12分
当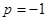 时,
时, . 13分
. 13分
综上所述,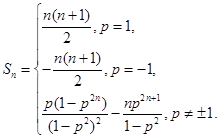 14分
14分
考点:本题主要考查等差数列、等比数列的的基础知识,公式求和法。
点评:中档题,本题具有较强的综合性,本解答从确定数列中项的关系入手,证明了数列是等比数列;通过分类讨论,根据数列的不同特征,利用“错位相减法”“公式法”求和。事实上,“分组求和法”“裂项相消法”也是高考考查的重点。


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:解答题
设数列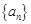 的前
的前 项和为
项和为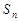 ,若对任意
,若对任意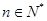 ,都有
,都有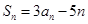 .
.
⑴求数列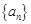 的首项;
的首项;
⑵求证:数列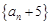 是等比数列,并求数列
是等比数列,并求数列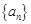 的通项公式;
的通项公式;
⑶数列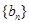 满足
满足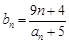 ,问是否存在
,问是否存在 ,使得
,使得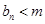 恒成立?如果存在,求出
恒成立?如果存在,求出 的值,如果不存在,说明理由.
的值,如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列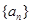 的前
的前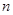 项和为
项和为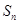 ,且有
,且有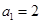 ,
,
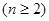 .
.
(Ⅰ)求数列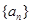 的通项公式;
的通项公式;
(Ⅱ)若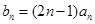 ,求数列
,求数列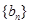 的前
的前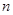 项和
项和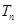 ;
;
(Ⅲ)若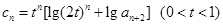 ,且数列
,且数列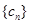 中的 每一项总小于它后面的项,求实数
中的 每一项总小于它后面的项,求实数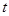 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com