
【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:

将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(1)根据已知条件完成下面的2×2列联表;
(2)根据此资料,判断是否有![]() 的把握认为“体育迷”与性别有关?
的把握认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
附: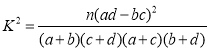 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
科目:高中数学 来源: 题型:
【题目】德阳中学数学竞赛培训共开设有初等代数、初等几何、初等数论和微积分初步共四门课程,要求初等代数、初等几何都要合格,且初等数论和微积分初步至少有一门合格,则能取得参加数学竞赛复赛的资格,现有甲、乙、丙三位同学报名参加数学竞赛培训,每一位同学对这四门课程考试是否合格相互独立,其合格的概率均相同,(见下表),且每一门课程是否合格相互独立,
课 程 | 初等代数 | 初等几何 | 初等数论 | 微积分初步 |
合格的概率 |
|
|
|
|
(1)求甲同学取得参加数学竞赛复赛的资格的概率;
(2)记![]() 表示三位同学中取得参加数学竞赛复赛的资格的人数,求
表示三位同学中取得参加数学竞赛复赛的资格的人数,求![]() 的分布列及期望
的分布列及期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放四十年以来,北京市居民生活发生了翻天覆地的变化.随着经济快速增长、居民收入稳步提升,消费结构逐步优化升级,生活品质显著增强,美好生活蓝图正在快速构建.北京市城镇居民人均消费支出从1998年的7 500元增长到2017年的40 000元.1998年与2017年北京市城镇居民消费结构对比如下图所示:

1998年北京市城镇居民消费结构 2017年北京市城镇居民消费结构
则下列叙述中不正确的是( )
A. 2017年北京市城镇居民食品支出占比同1998年相比大幅度降低
B. 2017年北京市城镇居民人均教育文化娱乐类支出同1998年相比有所减少
C. 2017年北京市城镇居民医疗保健支出占比同1998年相比提高约![]()
D. 2017年北京市城镇居民人均交通和通信类支出突破5 000元,大约是1998年的14倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某渔船在航行中不幸遇险,发出求救信号,我海军舰艇在A处获悉后,立即测出该渔船在方位角为45°、距离A为10海里的C处,并测得渔船正沿方位角105°的方向,以9海里/时的速度向某小岛B靠拢,我海军舰艇立即以21海里/时的速度前去营救,恰在小岛B处追上渔船.
(1)试问舰艇应按照怎样的航向前进?
(2)求出舰艇靠近渔船所用的时间?
(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题![]() 对任意
对任意![]() ,不等式
,不等式![]() 恒成立;命题q:存在
恒成立;命题q:存在![]() ,使得不等式
,使得不等式![]() 成立.
成立.
(1)若p为真命题,求实数m的取值范围;
(2)若命题p、q有且只有一个是真命题,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com