
【题目】按下面的流程图进行计算.若输出的![]() ,则输入的正实数
,则输入的正实数![]() 值的个数最多为( )
值的个数最多为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】程序框图的用途是数列求和,当x>100时结束循环,输出x的值为202:
当202=3x+1,解得x=67;即输入x=67时,输出结果202.
202=3(3x+1)+1,解得x=22;即输入x=22时,输出结果202.
202=3(3(3x+1)+1)+1.即201=3(3(3x+1)+1),
∴67=3(3x+1)+1,即22=3x+1,解得x=7,输入x=7时,输出结果202.
202=3(3(3(3x+1)+1)+1)+1.解得x=2,输入x=2时,输出结果202.
202=3(3(3(3(3x+1)+1)+1)+1)+1.解得x=![]() ,输入x=
,输入x=![]() 时,输出结果202.
时,输出结果202.
共有5个不同的x值。
故答案为A。


科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心为
的圆心为![]() ,直线
,直线![]() 过点
过点![]() 且与
且与![]() 轴不重合,
轴不重合, ![]() 交圆
交圆![]() 于
于![]() 两点,过
两点,过![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() .
.
(1)证明![]() 为定值,并写出点
为定值,并写出点![]() 的轨迹方程;
的轨迹方程;
(2)设![]() ,过点
,过点![]() 作直线
作直线![]() ,交点
,交点![]() 的轨迹于
的轨迹于![]() 两点 (异于
两点 (异于![]() ),直线
),直线![]() 的斜率分别为
的斜率分别为![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
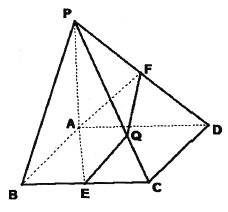
【题目】如图,在底面是菱形的四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,点
,点![]() 分别为
分别为![]() 的中点,设直线
的中点,设直线![]() 与平面
与平面![]() 交于点
交于点![]() .
.
(1)已知平面![]() 平面
平面![]() ,求证:
,求证: ![]() .
.
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
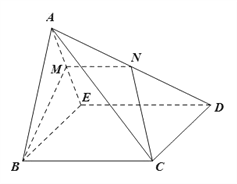
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,平面
为正方形,平面![]() 底面
底面![]() ,
, ![]() ,点
,点![]() 分别是
分别是![]() 的中点.
的中点.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() 平面
平面![]() ;
;
(Ⅲ)在棱![]() 上求作一点
上求作一点![]() ,使得
,使得![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
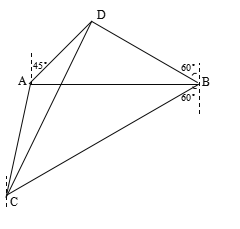
【题目】如图,A、B是海面上位于东西方向相距![]() 海里的两个观测点.现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号.位于B点南偏西60°且与B相距20
海里的两个观测点.现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号.位于B点南偏西60°且与B相距20![]() 海里的C点的救援船立即前往营救,其航行速度为30海里/小时。求救援船直线到达D的时间和航行方向.
海里的C点的救援船立即前往营救,其航行速度为30海里/小时。求救援船直线到达D的时间和航行方向.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若![]() ,
, ![]() 是椭圆
是椭圆![]() 上两个不同的动点,且使
上两个不同的动点,且使![]() 的角平分线垂直于
的角平分线垂直于![]() 轴,试判断直线
轴,试判断直线![]() 的斜率是否为定值?若是,求出该值;若不是,说明理由.
的斜率是否为定值?若是,求出该值;若不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com