练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    下列命题：
    ①四面体一定有外接球； ②四面体一定有内切球；③四面体任三个面的面积之和大于第四个面的面积；④四面体的四个面中最多有三个直角三角形；⑤四面体对棱中点的连线与另外四条棱异面．其中真命题的序号是    （填上所有真命题的序号）．
    【答案】分析：四面体一定有外接球和内切球；四面体任三个面的面积之和大于第四个面的面积；四面体的四个面中最多有四个直角三角形；四面体对棱中点的连线与另外四条棱是异面直线．
    解答：解：四面体一定有外接球和内切球，故①②都是真命题；
    四面体任三个面的面积之和大于第四个面的面积，故③是真命题；
    四面体的四个面中最多有四个直角三角形，
    如图，在四面体S-ABC中，AC⊥BC，AS⊥面ABC，
    由三垂线定理知，△ACB，△PAC，△PAB，△SCB都是直角三角形，

    故④是假命题；
    四面体对棱中点的连线与另外四条棱是异面直线，故⑤是真命题．
    故答案为：①②③⑤．
    点评：本题考查棱锥的结构特征，是基础题，解题时要认真审题，仔细解答．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    将边长为2，有一内角为60°的菱形ABCD沿较短对角线BD折成四面体ABCD，点E、F分别为AC、BD的中点，则下列命题中正确的是
    ②③④
    ②③④
    ；（将正确的命题序号全填上）．
    ①EF∥AB；
    ②EF与异面直线AC、BD都垂直；
    ③当四面体ABCD的体积最大时，AC=
    		6
    ；
    ④AC垂直于截面BDE．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2010•成都一模）如图，设A、B、C是球O面上的三点，我们把大圆的劣弧
    BC
    、
    CA
    、
    AB
    在球面上围成的部分叫做球面三角形，记作球面三角形ABC，在球面三角形ABC中，OA=1，设
    BC
    =a，
    CA
    =b，
    AB
    =c，a，b．c∈(0，π)    ，二面角B-OA-C、
    C-OB-A、A-OC-B的大小分别为α、β、γ，给出下列命题：
    ①若α=β=γ=
    π
    2
    ，则球面三角形ABC的面积为
    π
    2
    ；
    ②若a=b=c=
    π
    3
    ，则四面体OABC的侧面积为
    π
    2
    ；
    ③圆弧
    AB
    在点A处的切线l1与圆弧
    CA
    在点A处的切线l2的夹角等于a；
    ④若a=b，则α=β．
    其中你认为正确的所有命题的序号是
    ①②④
    ①②④
    ．

    查看答案和解析>>

    科目：高中数学 来源：2011年浙江省杭州市二中高二上学期期末考试数学理卷 题型：填空题

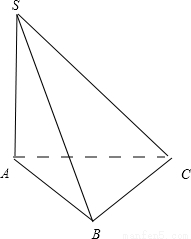
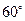    将边长为，有一内角为的菱形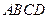沿较短对角线折成四面体，点 分别为的中点，则下列命题中正确的是         （将正确的命题序号全填上）：
    ①；②与异面直线、都垂直；③当四面体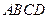的体积最大时，；
    ④垂直于截面.

    查看答案和解析>>

    科目：高中数学 来源：2011年浙江省杭州市高二上学期期末考试数学理卷 题型：填空题

    将边长为，有一内角为的菱形沿较短对角线折成四面体，点 分别为的中点，则下列命题中正确的是          （将正确的命题序号全填上）：

     ①； ②与异面直线、都垂直； ③当四面体的体积最大时，；

     ④垂直于截面.

     

    查看答案和解析>>

    科目：高中数学 来源：2013届山东省高二上学期期中理科数学试卷 题型：填空题

    将边长为，有一内角为的菱形沿较短对角线折成四面体，点 分别为的中点，则下列命题中正确的是          （将正确的命题序号全填上）．

     ①；

     ②与异面直线、都垂直；

     ③当四面体的体积最大时，；

     ④垂直于截面

     

     

    查看答案和解析>>

    同步练习册答案