
(本小题满分14分)
已知x=4是函数f(x)=alnx+x2-12x+11的一个极值点.
(1)求实数a的值;
(2)求函数f(x)的单调区间;
(3)若直线y=b与函数y=f(x)的图象有3个交点,求b的取值范围.
(1)∵f′(x)=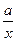 +2x-12,
+2x-12,
∴f′(4)=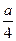 +8-12=0
+8-12=0
因此a=16 ……………………………………………3分
(2)由(1)知,
f(x)=16lnx+x2-12x+11,x∈(0,+∞)
f′(x)=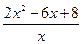 …………………………5分
…………………………5分
当x∈(0,2)∪(4,+∞)时,f′(x)>0
当x∈(2,4)时,f′(x)<0……………………………………………7分
所以f(x)的单调增区间是(0,2),(4,+∞)
f(x)的单凋减区间是(2,4) ……………………………………………………………………8分
(3)由(2)知,f(x)在(0,2)内单调增加,在(2,4)内单调减少,在(4,+∞)上单调增加,且当x=2或x=4时,f′(x)=0
所以f(x)的极大值为f(2)=16ln2-9,极小值为f(4)=32ln2-21
因此f(16)=16ln16+162-12×16+11>16ln2-9=f(2)
f(e-2)<-32+11=-21<f(4)
所以在f(x)的三个单调区间(0,2),(2,4) ,(4,+∞)内,直线y=b与y=f(x)的图象各有一个交点,
当且仅当f(4)<b<f(2)成立………………………………………………………………………………13分
因此,b的取值范围为(32 ln2-21,16ln2-9). …………………………………………………………14分
解析


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
(本题15分)已知函数 是奇函数,且图像在点
是奇函数,且图像在点
 为自然对数的底数)处的切线斜率为3.
为自然对数的底数)处的切线斜率为3.
(1) 求实数 、
、 的值;
的值;
(2) 若 ,且
,且 对任意
对任意 恒成立,求
恒成立,求 的最大值;
的最大值;
(3) 当 时,证明:
时,证明:
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
设函数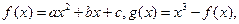 (
(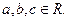 )若
)若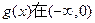 上是增函数,在(0,1)上是减函数,函数
上是增函数,在(0,1)上是减函数,函数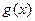 在R上有三个零点,且1是其中一个零点。
在R上有三个零点,且1是其中一个零点。
(1)求b的值;
(2)求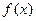 最小值的取值范围。
最小值的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂生产某种产品,已知该产品的月生产量 (吨)与每吨产品的价格p(元/吨)之间的关系式为:p=24200-0.2x2,且生产x吨的成本为
(吨)与每吨产品的价格p(元/吨)之间的关系式为:p=24200-0.2x2,且生产x吨的成本为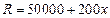 (元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(注:利润=收入─成本)
(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(注:利润=收入─成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com