练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

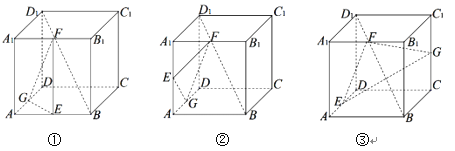
    【题目】如图，在下列三个正方体中，均为所在棱的中点，过作正方体的截面．在各正方体中，直线与平面的位置关系描述正确的是

    A. 平面的有且只有①；平面的有且只有②③

    B. 平面的有且只有②；平面的有且只有①

    C. .平面的有且只有①；平面的有且只有②

    D. 平面的有且只有②；平面的有且只有③

    【答案】A

    【解析】

    ①连结，根据面面平行的判定定理可证平面平面，进而可得平面；

    ②③都可以根据线面垂直的判定定理，用向量的方法分别证明，，即可证明平面；从而可得出结果.

    ①连结，因为均为所在棱的中点，所以，，从而可得平面，平面；根据，可得平面平面；所以平面；

    ②设正方体棱长为，因为均为所在棱的中点，

    所以，即；

    又，即；

    又，所以平面；

    ③设正方体棱长为，因为均为所在棱的中点，

    所以，即；

    又，即；

    又，所以平面；

    故选A

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】函数，其中常数.

    （1）求的最小值；

    （2）若，讨论的零点的个数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，点为正四棱锥的底面中心，四边形为矩形，且，．

    （1）求正四棱锥的体积；

    （2）设为侧棱上的点，且，求直线和平面所成角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，以坐标原点务极点，轴正半轴为极轴建立极坐标系，曲线，

    (1)求曲线，的直角坐标方程；

    (2)曲线和的交点为，，求以为直径的圆与轴的交点坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】根据统计调查数据显示：某企业某种产品的质量指标值服从正态分布，从该企业生产的这种产品（数量很大）中抽取100件，测量这100件产品的质量指标值，由测量结果得到如图所示的频率分布直方图，质量指标值落在区间，，内的频率之比为.

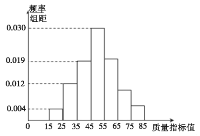
    （1）求这100件产品质量指标值落在区间内的频率；

    （2）根据频率分布直方图求平均数（同一组中的数据用该组区间的中点值作代表）；

    （3）若取这100件产品指标的平均值，从这种产品（数量很大）中任取3个，求至少有1个落在区间的概率.

    参考数据：，若，则；；.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平行四边形中，，.现沿对角线将折起，使点到达点.点、分别在、上，且、、、四点共面.

    （1）求证：；

    （2）若平面平面，平面与平面夹角为，求与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，a∈R．

    （Ⅰ）当a=1时，求曲线y=f（x）在点（0，f（0））处的切线方程；

    （Ⅱ）求f（x）的单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示的多面体中，四边形为菱形，且，为的中点．

    （1）求证：平面；

    （2）若平面平面，求直线与平面所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中,对于点,定义变换:将点变换为点,使得其中.这样变换就将坐标系内的曲线变换为坐标系内的曲线.则四个函数,,,在坐标系内的图象,变换为坐标系内的四条曲线（如图）依次是

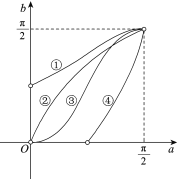
    A. ②,③,①,④B. ③,②,④,①C. ②,③,④,①D. ③,②,①,④

    查看答案和解析>>

    同步练习册答案