
 (a,b为常数),且方程
(a,b为常数),且方程 有两个实根为x1=-1,x2=2,
有两个实根为x1=-1,x2=2, 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源:2012-2013学年安徽省黄山市屯溪一中高三(上)10月月考数学试卷(理科)(解析版) 题型:解答题
 (a,b为常数),且方程
(a,b为常数),且方程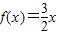 有两个实根为x1=-1,x2=2,
有两个实根为x1=-1,x2=2,查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省郑州市新密二高高三(上)第一次月考数学试卷(解析版) 题型:解答题
 (a,b为常数),且方程
(a,b为常数),且方程 有两个实根为x1=-1,x2=2,
有两个实根为x1=-1,x2=2,查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省益阳市南县一中高三(上)8月月考数学试卷(理科)(解析版) 题型:解答题
 (a,b为常数),且方程
(a,b为常数),且方程 有两个实根为x1=-1,x2=2,
有两个实根为x1=-1,x2=2,查看答案和解析>>
科目:高中数学 来源:2012年云南省曲靖市宣威市高三第一次调研摸底数学试卷(理科)(解析版) 题型:解答题
 (a,b为常数),且方程
(a,b为常数),且方程 有两个实根为x1=-1,x2=2,
有两个实根为x1=-1,x2=2,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com