解:以圆拱拱顶为坐标原点,以过拱顶顶点的竖直直线为y轴,建立直角坐标系,
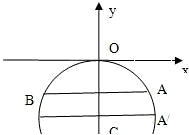
设圆心为C,水面所在弦的端点为A,B,则由已知可得:A(6,-2),
设圆的半径为r,则C(0,-r),即圆的方程为x
2+(y+r)
2=r
2将A的坐标代入圆的方程可得r=10
所以圆的方程是:x
2+(y+10)
2=100
则当水面下降1米后可设A′的坐标为(x
0,-3)(x
0>0)
代入圆的方程可得x
0=

,
所以当水面下降1米后,水面宽为2

米.
分析:先根据题目条件建立适当的直角坐标系,得到各点的坐标,通过设圆的半径,可得圆的方程,然后将点的坐标代入确定圆的方程,设当水面下降1米后可设A′的坐标为(x
0,-3)(x
0>0)根据点在圆上,可求得x
0的值,从而得到问题的结果.
点评:本题考查了圆的方程的综合应用,以及点在圆上的条件的转化,圆的对称性的体现,是个基础题.


 设圆心为C,水面所在弦的端点为A,B,则由已知可得:A(6,-2),
设圆心为C,水面所在弦的端点为A,B,则由已知可得:A(6,-2), ,
, 米.
米.
