
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:填空题
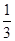 [k(k+1)(k+2)-(k-1)k(k+1)],
[k(k+1)(k+2)-(k-1)k(k+1)],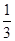 (1×2×3-0×1×2),
(1×2×3-0×1×2),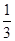 (2×3×4-1×2×3),…,
(2×3×4-1×2×3),…,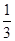 [n(n+1)(n+2)-(n-1)n(n+1)].
[n(n+1)(n+2)-(n-1)n(n+1)].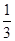 n(n+1)(n+2).
n(n+1)(n+2).查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
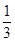 +
+ =1;
=1;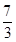 +
+ +
+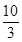 +
+ =12;
=12;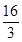 +
+ +
+ +
+ +
+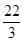 +
+ =39;
=39; +
+ +
+ +
+ +…+
+…+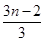 +
+ =________(最后结果用m,n表示).
=________(最后结果用m,n表示).查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
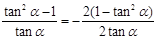
 =-
=-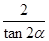 ①
①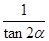 =-
=-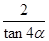 ②
②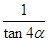 =-
=-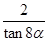 ③
③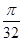 +2tan
+2tan +4tan
+4tan -
-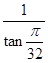 =( )
=( )| A.-2 | B.-4 | C.-6 | D.-8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com