
【题目】已知函数f(x)=|x+a|+|x+ ![]() |(a>0)(a<0)
|(a>0)(a<0)
(1)当a=2时,求不等式f(x)>3的解集
(2)证明: ![]() .
.
【答案】
(1)解:当a=2时,f(x)=|x+2|+|x+ ![]() |,原不等式等价于
|,原不等式等价于 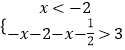
或 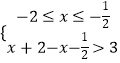 或
或 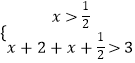
解得:x<﹣ ![]() 或x∈或
或x∈或 ![]() ,所以不等式的解集为{x|x<﹣
,所以不等式的解集为{x|x<﹣ ![]() 或
或 ![]()
(2)解:f(m)+f(﹣ ![]() )=|m+a|+|m+
)=|m+a|+|m+ ![]() |+|﹣
|+|﹣ ![]() +a|+|﹣
+a|+|﹣ ![]() +
+ ![]() |
|
= ![]()
【解析】(1)分类讨论,解不等式,即可得出结论;(2)f(m)+f(﹣ ![]() )=|m+a|+|m+
)=|m+a|+|m+ ![]() |+|﹣
|+|﹣ ![]() +a|+|﹣
+a|+|﹣ ![]() +
+ ![]() |,利用三角不等式,及基本不等式即可证明结论.
|,利用三角不等式,及基本不等式即可证明结论.
【考点精析】解答此题的关键在于理解绝对值不等式的解法的相关知识,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号,以及对不等式的证明的理解,了解不等式证明的几种常用方法:常用方法有:比较法(作差,作商法)、综合法、分析法;其它方法有:换元法、反证法、放缩法、构造法,函数单调性法,数学归纳法等.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】设双曲线 ![]() (a>0,b>0)的左焦点为F1 , 左顶点为A,过F1作x轴的垂线交双曲线于P、Q两点,过P作PM垂直QA于M,过Q作QN垂直PA于N,设PM与QN的交点为B,若B到直线PQ的距离大于a+
(a>0,b>0)的左焦点为F1 , 左顶点为A,过F1作x轴的垂线交双曲线于P、Q两点,过P作PM垂直QA于M,过Q作QN垂直PA于N,设PM与QN的交点为B,若B到直线PQ的距离大于a+ ![]() ,则该双曲线的离心率取值范围是( )
,则该双曲线的离心率取值范围是( )
A.(1﹣ ![]() )
)
B.( ![]() ,+∞)
,+∞)
C.(1,2 ![]() )
)
D.(2 ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
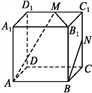
【题目】如图所示,在正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,有以下四个结论:
①直线AM与CC1是相交直线;②直线AM与BN是平行直线;
③直线BN与MB1是异面直线; ④直线MN与AC所成的角为60°.
其中正确的结论为___ (注:把你认为正确的结论序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C1的圆心在坐标原点O,且恰好与直线![]() 相切.
相切.
(Ⅰ)求圆C1的标准方程;
(Ⅱ)设点A为圆上一动点,AN垂直于x轴于点N,若动点Q满足![]()
(其中m为非零常数),试求动点Q的轨迹方程;
(Ⅲ)在(Ⅱ)的结论下,当m=![]() 时,得到动点Q的轨迹为曲线C,与l1垂直的直线l与曲线C交于B,D两点,求△OBD面积的最大值.
时,得到动点Q的轨迹为曲线C,与l1垂直的直线l与曲线C交于B,D两点,求△OBD面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (
( ![]() 为实常数).
为实常数).
(1)若 ![]() ,
, ![]() ,求
,求 ![]() 的单调区间;
的单调区间;
(2)若 ![]() ,且
,且 ![]() ,求函数
,求函数 ![]() 在
在 ![]() 上的最小值及相应的
上的最小值及相应的 ![]() 值;
值;
(3)设 ![]() ,若存在
,若存在 ![]() ,使得
,使得 ![]() 成立,求实数
成立,求实数 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机调查询问110名性别不同的高中生是否爱好某项运动,得到如下的列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由 ![]() 计算得
计算得 ![]()
附表:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
C.有99%以上的把握认为“爱好该项运动与性别无关”
D.有99%以上的把握认为“爱好该项运动与性别有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)当 ![]() 时,求
时,求 ![]() 的单调区间;
的单调区间;
(2)设 ![]() ,
, ![]() 是曲线
是曲线 ![]() 图象上的两个相异的点,若直线
图象上的两个相异的点,若直线 ![]() 的斜率
的斜率 ![]() 恒成立,求实数
恒成立,求实数 ![]() 的取值范围;
的取值范围;
(3)设函数 ![]() 有两个极值点
有两个极值点 ![]() ,
, ![]() ,且
,且 ![]() ,若
,若 ![]() 恒成立,求实数
恒成立,求实数 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠ABC=∠BAD=90°,![]() ,
,![]() ,F分别为AB,PC的中点.
,F分别为AB,PC的中点.
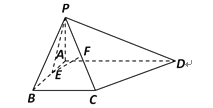
(I)若四棱锥P-ABCD的体积为4,求PA的长;
(II)求证:PE⊥BC;
(III)求PC与平面PAD所成角的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com