
| A. | ①②④ | B. | ②③⑤ | C. | ①③④ | D. | ①②⑤ |
分析 由系统抽样方法判断①;写出命题的否定判断②;利用辅助角公式化积,再由三角函数的图象平移判断③;由幂函数的概念及性质判断④;由等比数列的概念判断⑤.
解答 解:①从编号为001,002,…,500的500个产品中用系统抽样的方法抽取一个样本,已知样本编号从小到大依次为007,032,…,可知分段间隔为25,抽取20个样本,则样本中最大的编号是7+25×19=482,故①正确;
②命题“?x∈R,均有x2-3x-2>0”的否定是:“?x0∈R,使得x02-3x0-2≤0”,故②正确;
③将函数$y=\sqrt{3}cosx+sinx(x∈R)$=$2sin(x+\frac{π}{6})$的图象向右平移$\frac{π}{6}$后,所得到的图象对应的函数解析式为y=2sinx,关于原点中心对称,故③错误;
④若$f(x)=({m-1})•{x^{{m^2}-4m+3}}$是幂函数,则m-1=1,即m=2,则m2-4m+3=-1,则在(0,+∞)上递减,故④错误;
⑤如果{an}为等比数列,设其公比为q,且bn=a2n-1+a2n+1,则$\frac{{b}_{n+1}}{{b}_{n}}=\frac{{a}_{2n+1}+{a}_{2n+3}}{{a}_{2n-1}+{a}_{2n+1}}=\frac{{q}^{2}({a}_{2n-1}+{a}_{2n+1})}{{a}_{2n-1}+{a}_{2n+1}}={q}^{2}$,
∴数列{bn}也是等比数列,故⑤正确.
∴正确的命题是①②⑤.
故选:D.
点评 本题考查命题的真假判断与应用,考查系统抽样方法、命题的否定、三角函数的图象平移、幂函数及等比数列的概念,是基础题.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
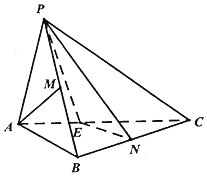 如图,三棱锥P-ABC中,BC⊥平面PAB,PA=PB=AB=6,BC=9,点M,N分别为PB,BC的中点.
如图,三棱锥P-ABC中,BC⊥平面PAB,PA=PB=AB=6,BC=9,点M,N分别为PB,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不存在x0∈R,${x_0}^2-2{x_0}+1≥0$ | B. | 存在x0∈R,${x_0}^2-2{x_0}+1≤0$ | ||
| C. | 存在x0∈R,${x_0}^2-2{x_0}+1<0$ | D. | 对任意的x∈R,x2-2x+1<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com