
【题目】已知函数f(x)=lnx,g(x)= ![]() x2﹣bx(b为常数).
x2﹣bx(b为常数).
(1)函数f(x)的图象在点(1,f(1))处的切线与函数g(x)的图象相切,求实数b的值;
(2)若函数h(x)=f(x)+g(x)在定义域上存在单调减区间,求实数b的取值范围;
(3)若b≥2,x1 , x2∈[1,2],且x1≠x2 , 都有|f(x1)﹣f(x2)|>|g(x1)﹣g(x2)|成立,求实数b的取值范围.
【答案】
(1)解:因为f(x)=lnx,所以 ![]() ,因此f'(1)=1,
,因此f'(1)=1,
所以函数f(x)的图象在点(1,f(1))处的切线方程为y=x﹣1,
由 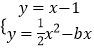 得x2﹣2(b+1)x+2=0.
得x2﹣2(b+1)x+2=0.
由△=4(b+1)2﹣8=0,得 ![]() .
.
(还可以通过导数来求b)
(2)解:因为h(x)=f(x)+g(x)= ![]() (x>0),
(x>0),
所以 ![]() ,
,
由题意知h'(x)<0在(0,+∞)上有解,
因为x>0,设u(x)=x2﹣bx+1,因为u(0)=1>0,
则只要  ,解得b>2,
,解得b>2,
所以b的取值范围是(2,+∞)
(3)解:不妨设x1>x2,
因为函数f(x)=lnx在区间[1,2]上是增函数,
所以f(x1)>f(x2),
函数g(x)图象的对称轴为x=b,且b>2.
当b≥2时,函数g(x)在区间[1,2]上是减函数,
所以g(x1)<g(x2),
所以|f(x1)﹣f(x2)|>|g(x1)﹣g(x2)|,
等价于f(x1)﹣f(x2)>g(x2)﹣g(x1),
即f(x1)+g(x1)>f(x2)+g(x2),
等价于h(x)=f(x)+g(x)= ![]() 在区间[1,2]上是增函数,
在区间[1,2]上是增函数,
等价于 ![]() 在区间[1,2]上恒成立,
在区间[1,2]上恒成立,
等价于 ![]() 在区间[1,2]上恒成立,所以b≤2,又b≥2,所以b=2
在区间[1,2]上恒成立,所以b≤2,又b≥2,所以b=2
【解析】(1)求出函数的导数根据二次函数的性质求出b的值即可;(2)求出h(x)的导数,结合二次函数的性质得到关于b的不等式组,解出即可;(3)问题等价于f(x1)﹣f(x2)>g(x2)﹣g(x1),即h(x)=f(x)+g(x)= ![]() 在区间[1,2]上是增函数,根据函数的单调性求出b的范围即可.
在区间[1,2]上是增函数,根据函数的单调性求出b的范围即可.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


科目:高中数学 来源: 题型:
【题目】已知整数n≥4,集合M={1,2,3,…,n}的所有含有4个元素的子集记为A1 , A2 , A3 , …, ![]() .
.
设A1 , A2 , A3 , …, ![]() 中所有元素之和为Sn .
中所有元素之和为Sn .
(1)求S4 , S5 , S6并求出Sn;
(2)证明:S4+S5+…+Sn=10Cn+26 .
查看答案和解析>>
科目:高中数学 来源: 题型:
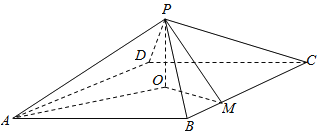
【题目】如图,在四棱锥![]() 中,底面是以O为中心的菱形,
中,底面是以O为中心的菱形,![]() 底面ABCD,
底面ABCD,![]() ,
,![]() ,M为BC上一点.
,M为BC上一点.
![]() 当BM等于多少时,
当BM等于多少时,![]() 平面POM?
平面POM?
![]() 在满足
在满足![]() 的条件下,若
的条件下,若![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】去年“十一”期间,昆曲高速公路车辆较多.某调查公司在曲靖收费站从7座以下小型汽车中按进收费站的先后顺序,每间隔50辆就抽取一辆的抽样方法抽取40辆汽车进行抽样调查,将他们在某段高速公路的车速(![]() )分成六段:
)分成六段:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 后,得到如图的频率分布直方图.
后,得到如图的频率分布直方图.

(I)调查公司在抽样时用到的是哪种抽样方法?
(II)求这40辆小型汽车车速的众数和中位数的估计值;
(III)若从这40辆车速在![]() 的小型汽车中任意抽取2辆,求抽出的2辆车车速都在
的小型汽车中任意抽取2辆,求抽出的2辆车车速都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围为[0,10],分为五个级别,T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如右图. (Ⅰ)这50个路段为中度拥堵的有多少个?
(Ⅱ)据此估计,早高峰三环以内的三个路段至少有一个是严重拥堵的概率是多少?
(III)某人上班路上所用时间若畅通时为20分钟,基本畅通为30分钟,轻度拥堵为36分钟;中度拥堵为42分钟;严重拥堵为60分钟,求此人所用时间的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究小组欲研究昼夜温差大小与患感冒人数之间的关系,统计得到1至6月份每月9号的昼夜温差![]() 与因患感冒而就诊的人数
与因患感冒而就诊的人数![]() 的数据,如下表:
的数据,如下表:
日期 | 1月9号 | 2月9号 | 3月9号 | 4月9号 | 5月9号 | 6月9号 |
| 10 | 11 | 13 | 12 | 8 | 6 |
| 22 | 25 | 29 | 26 | 16 | 12 |
该研究小组的研究方案是:先从这6组数据中选取2组,用剩下的4组数据求回归方程,再用之前被选取的2组数据进行检验.
(1)若选取1月和6月的数据作为检验数据,请根据剩下的2至5月的数据,求出![]() 关于
关于![]() 的线性回归方程;(计算结果保留最简分数)
的线性回归方程;(计算结果保留最简分数)
(2)若用(1)中所求的回归方程作预报,得到的估计数据与所选出的检验数据的误差不超过2人,则认为得到的回归方程是理想的,试问该研究小组所得回归方程是否理想?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=asinωx+bcosωx(0<ω<5,ab≠0)的图象的一条对称轴方程是 ![]() ,函数f'(x)的图象的一个对称中心是
,函数f'(x)的图象的一个对称中心是 ![]() ,则f(x)的最小正周期是( )
,则f(x)的最小正周期是( )
A.![]()
B.![]()
C.π
D.2π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com