
 | (0,2] | (2,3] | (3,4] | (4,5] |
| 甲 | $\frac{1}{2}$ | x | x | x |
| 乙 | $\frac{1}{6}$ | $\frac{1}{3}$ | y | 0 |
分析 (1)首先求出x、y,个人停车所付费用相同即停车时间相同:都不超过两小时、都在两小时以上且不超过三小时和都超过三小时且不超过四小时三类求解即可.
(2)随机变量ξ的所有取值为0,1、2,3,4,5,由独立事件的概率分别求概率,列出分布列,再由期望的公式求期望即可.
解答 解:(1)由题意得$\frac{1}{2}+3x=1∴x=\frac{1}{6}$.
$\frac{1}{6}+\frac{1}{3}+y=1∴y=\frac{1}{2}$.
记甲乙两人所付车费相同的事件为A,P(A)=$\frac{1}{2}×\frac{1}{6}+\frac{1}{6}×\frac{1}{3}+\frac{1}{6}×\frac{1}{2}=\frac{2}{9}$,
甲、乙两人所付车费相同的概率为$\frac{2}{9}$.
(2)设甲、乙两人所付停车费之和为随机变量ξ,ξ的所有取值为0,1、2,3,4,5.
P(ξ=0)=$\frac{1}{12}$,P(ξ=1)=$\frac{1}{2}×\frac{1}{3}+\frac{1}{6}×\frac{1}{6}=\frac{7}{36}$,P(ξ=2)=$\frac{1}{6}×\frac{1}{6}+\frac{1}{6}×\frac{1}{3}+\frac{1}{2}×\frac{1}{2}=\frac{1}{3}$,
P(ξ=3)=$\frac{1}{6}×\frac{1}{6}+\frac{1}{6}×\frac{1}{3}+\frac{1}{6}×\frac{1}{2}=\frac{1}{6}$
P(ξ=4)=$\frac{1}{6}×\frac{1}{2}+\frac{1}{6}×\frac{1}{3}=\frac{5}{36}$,P(ξ=5)=$\frac{1}{6}×\frac{1}{2}=\frac{1}{12}$.
所以ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{1}{12}$ | $\frac{7}{36}$ | $\frac{1}{3}$ | $\frac{1}{6}$ | $\frac{5}{36}$ | $\frac{1}{12}$ |
点评 本题考查独立事件、互斥事件的概率、离散型随机变量的分布列和数学期望,考查利用所学知识解决问题的能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
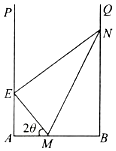 某地拟在一个U形水面PABQ(∠A=∠B=90°)上修一条堤坝(E在AP上,N在BQ上),围出一个封闭区域EABN,用以种植水生植物.为了美观起见,决定从AB上点M处分别向点E,N拉2条分割线ME,MN,将所围区域分成3个部分(如图),每部分种植不同的水生植物.已知AB=a,EM=BM,∠MEN=90°,设所拉分割线总长度为l.
某地拟在一个U形水面PABQ(∠A=∠B=90°)上修一条堤坝(E在AP上,N在BQ上),围出一个封闭区域EABN,用以种植水生植物.为了美观起见,决定从AB上点M处分别向点E,N拉2条分割线ME,MN,将所围区域分成3个部分(如图),每部分种植不同的水生植物.已知AB=a,EM=BM,∠MEN=90°,设所拉分割线总长度为l.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{2π}{3}$ | C. | -$\frac{5π}{6}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{204}$ | B. | $\frac{45}{68}$ | C. | $\frac{15}{68}$ | D. | $\frac{5}{68}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{7}{8}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com