练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】为彻底打赢脱贫攻坚战，2020年春，某市政府投入资金帮扶某农户种植蔬菜大棚脱贫致富，若该农户计划种植冬瓜和茄子，总面积不超过15亩，帮扶资金不超过4万元，冬瓜每亩产量10 000斤，成本2000元，每斤售价0.5元，茄子每亩产量5000斤，成本3000元，每斤售价1.4元，则该农户种植冬瓜和茄子利润的最大值为（ ）

    A.4万元B.5.5万元C.6.5万元D.10万元

    【答案】B

    【解析】

    设种植冬瓜和茄子的种植面积分别为，亩，种植总利润为万元，然后根据题意建立关于与的约束条件，得到目标函数，利用线性规划的知识求出最值即可.

    设种植冬瓜和茄子的种植面积分别为，亩，种植总利润为万元，

    由题意可知，

    总利润

    作出约束条件如下图阴影部分：

    联立解得，

    平移直线，当过点时，一年的种植总利润为取最大值5.5万元，

    故选：B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】2020年春节前后，一场突如其来的新冠肺炎疫情在武汉出现并很快地传染开来(已有证据表明2019年10月、11月国外已经存在新冠肺炎病毒)，人传人，传播快，传播广，病亡率高，对人类生命形成巨大危害.在中华人民共和国，在中共中央、国务院强有力的组织领导下，全国人民万众一心抗击、防控新冠肺炎，疫情早在3月底已经得到了非常好的控制(累计病亡人数3869人).然而，国外因国家体制、思想观念与中国的不同，防控不力，新冠肺炎疫情越来越严重.据美国约翰斯·霍普金斯大学每日下午6时公布的统计数据，选取5月6日至5月10日的美国的新冠肺炎病亡人数如下表(其中t表示时间变量，日期“5月6日”、“5月7日”对应于“t=6"、“t=7"，依次下去)，由下表求得累计病亡人数与时间的相关系数r=0.98.

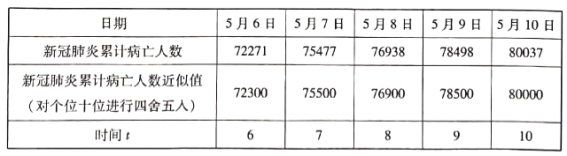
    （1）在5月6日~10日，美国新冠肺炎病亡人数与时间(日期)是否呈现线性相关性?

    （2）选择对累计病亡人数四舍五入后个位、十位均为0的近似数，求每日累计病亡人数y随时间t变化的线性回归方程；

    （3）请估计美国5月11日新冠肺炎病亡累计人数，请初步预测病亡人数达到9万的日期.

    附:回归方程中斜率和截距最小二乘估计公式分别为

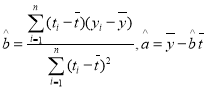
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设抛物线的焦点为，点是上一点，且线段的中点坐标为.

    （1）求抛物线的标准方程；

    （2）若，为抛物线上的两个动点（异于点），且，求点的横坐标的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年末，武汉出现新型冠状病毒肺炎（）疫情，并快速席卷我国其他地区，传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株，所以目前没有特异治疗方法，防控难度很大.武汉市出现疫情最早，感染人员最多，防控压力最大，武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和与确诊患者的密切接触者等“四类”人员，强化网格化管理，不落一户、不漏一人.在排查期间，一户6口之家被确认为“与确诊患者的密切接触者”，这种情况下医护人员要对其家庭成员随机地逐一进行“核糖核酸”检测，若出现阳性，则该家庭为“感染高危户”.设该家庭每个成员检测呈阳性的概率均为（）且相互独立，该家庭至少检测了5个人才能确定为“感染高危户”的概率为，当时，最大，则（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱ABC－A1B1C1中，侧面ABB1A1为菱形，D为AB的中点，为等腰三角形，∠ACB＝，∠ABB1＝，且AB＝B1C.

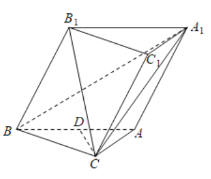
    （1）证明：CD⊥平面ABB1A1 ；

    （2）求CD与平面A1BC所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（自然对数的底数）有两个零点.

    （1）求实数的取值范围；

    （2）若的两个零点分别为，证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】学业水平测试成绩按照考生原始成绩从高到低分为五个等级.某班共有名学生且全部选考物理、化学两科，这两科的学业水平测试成绩如表所示.该班学生中，这两科等级均为的学生有人，这两科中仅有一科等级为的学生，其另外一科等级为.则该班（ ）

    等级

    科目

    A

    B

    C

    D

    E

    物理

    10

    16

    9

    1

    0

    化学

    8

    19

    7

    2

    0

    A.物理化学等级都是的学生至多有人

    B.物理化学等级都是的学生至少有人

    C.这两科只有一科等级为且最高等级为的学生至多有人

    D.这两科只有一科等级为且最高等级为的学生至少有人

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C：（a＞b＞0）的焦距为2，且过点.

    （1）求椭圆C的方程；

    （2）已知△BMN是椭圆C的内接三角形，若坐标原点O为△BMN的重心，求点O到直线MN距离的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的焦点为，为坐标原点，过点的直线与交于、两点.

    （1）若直线与圆相切，求直线的方程；

    （2）若直线与轴的交点为，且，，试探究：是否为定值.若为定值，求出该定值，若不为定值，试说明理由.

    查看答案和解析>>

    同步练习册答案