已知f(x)=x2+(lga+2)x+lgb,f(-1)=-2,当x∈R时,f(x)≥2x恒成立,
(1)求实数a,b的值.
(2)求y=f(x)在[t,t+2]上的最小值g(t).
解:由f(-1)=-2,得:f(-1)=1-(lga+2)+lgb=-2,化简得:lga-lgb=1,
∴

=10,a=10b.
又由x∈R,f(x)≥2x恒成立.知:x
2+(lga+2)x+lgb≥2x,即x
2+xlga+lgb≥0对x∈R恒成立,
由△=lg
2a-4lgb≤0,得(1+lgb)
2-4lgb≤0,
即(lgb-1)
2≤0,只有lgb=1,不等式成立,即b=10,∴a=100.
(2)f(x)=x
2+4x+1=(2+x)
2-3,
当t+2≤-2即t≤-4时,f(x)在[t,t+2]上递减,g(t)=f(t+2)=t
2+8t+13;
当t<-2<t+2即-4<t<-2时,g(t)=f(-2)=-3;
当t≥-2时,f(x)在[t,t+2]上递增,g(t)=f(t)=t
2+4t+1;
所以
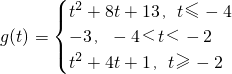
.
分析:(1)由f(-1)=-2得a,b的方程①,由f(x)≥2x即恒成立x
2+xlga+lgb≥0对x∈R恒成立,得△=lg
2a-4lgb≤0,消掉a得b的不等式,由此可得关于b的方程,从而得到b值,进而得到a值;
(2)由(1)可知f(x)=x
2+4x+1=(2+x)
2-3,按照对称轴在区间左侧、内部、右侧三种情况分类讨论,借助图象可得其最小值;
点评:本题考查二次函数的性质、二次函数在闭区间上的最值及函数恒成立问题,考查分类讨论思想、数形结合思想,关于二次函数在闭区间上的最值求解,往往借助图象加以分析.

 =10,a=10b.
=10,a=10b.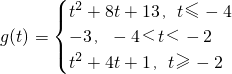 .
.

 阅读快车系列答案
阅读快车系列答案