
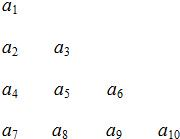 ������{an}�е������ÿһ�б���һ�ж�һ��Ĺ����ų�����������a1a2a3a4a5a6a7a8a9a10���DZ��еĵ�һ����a1��a2��a4��a7�������ɵ�����Ϊ{bn}��b1=a1=1��SnΪ����{bn}��ǰn��ͣ�������
������{an}�е������ÿһ�б���һ�ж�һ��Ĺ����ų�����������a1a2a3a4a5a6a7a8a9a10���DZ��еĵ�һ����a1��a2��a4��a7�������ɵ�����Ϊ{bn}��b1=a1=1��SnΪ����{bn}��ǰn��ͣ�������| 2bn | ||
bnSn-
|
| 1 |
| Sn |
| 4 |
| 91 |
| 2bn | ||
bnSn-
|
| 2(Sn-Sn-1) | ||
(Sn-Sn-1)Sn-
|
| 2(Sn-Sn-1) |
| -Sn-1Sn |
| 1 |
| Sn |
| 1 |
| Sn-1 |
| 1 |
| 2 |
| 1 |
| Sn |
| 1 |
| 2 |
| 1 |
| Sn |
| 1 |
| 2 |
| n+1 |
| 2 |
| 2 |
| n+1 |
| 2 |
| n+1 |
| 2 |
| n |
| 2 |
| n(n+1) |
|
| 12��13 |
| 2 |
| 4 |
| 91 |
| 2 |
| 13��14 |
| bk(1-qk) |
| 1-q |
| 2 |
| k(k+1) |
| (1-2k) |
| 1-2 |
| 2 |
| k(k+1) |


 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
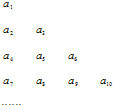 ������{an}�е������ÿһ�б���һ�ж�һ��Ĺ����ų����±���
������{an}�е������ÿһ�б���һ�ж�һ��Ĺ����ų����±���| 2bn | ||
bnSn-
|
| 1 |
| Sn |
| 4 |
| 91 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ������{an}�е������ÿһ�б���һ�ж�һ��Ĺ����ų������������DZ��е�һ����a1��a2��a4��a7�������ɵ�����Ϊ{bn}��b1=a1=1��SnΪ����{bn}��ǰn��ͣ�������2bn=bnSn-Sn2��n��2��n��N*����
������{an}�е������ÿһ�б���һ�ж�һ��Ĺ����ų������������DZ��е�һ����a1��a2��a4��a7�������ɵ�����Ϊ{bn}��b1=a1=1��SnΪ����{bn}��ǰn��ͣ�������2bn=bnSn-Sn2��n��2��n��N*����| 1 |
| Sn |
| 4 |
| 91 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ������{an}�е������ÿһ�б���һ�ж�һ��Ĺ����ų����±���
������{an}�е������ÿһ�б���һ�ж�һ��Ĺ����ų����±���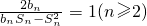 ��
��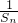 �ɵȲ����У���������{bn}��ͨ�ʽ��
�ɵȲ����У���������{bn}��ͨ�ʽ��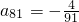 ʱ������q��ֵ��
ʱ������q��ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011�꽭��ʡ�����к�����ѧ�߿���ѧģ���Ծ���3���������棩 ���ͣ������

 ��bΪ���ڵ���3������������������{cn}���Ƿ������������ɵȱ����У������ڣ�������гɵȱ����е���������������ڣ���˵�����ɣ�
��bΪ���ڵ���3������������������{cn}���Ƿ������������ɵȱ����У������ڣ�������гɵȱ����е���������������ڣ���˵�����ɣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com