已知椭圆:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的左右焦点分别为F1.F2(1.0).且过点$$.右顶点为A.经过点F2的动直线l与椭圆交于B.C两点．(1)求椭圆方程,(2)记△AOB和△AOC的面积分别为S1和S2.求|S1-S2|的最大值,(3)在x轴上是否存在一点T.使得点B关于x轴的对称点落在直线TC上?若存在.则求出T点坐标,若不存在.请说明理由� 题目和参考答案——青夏教育精英家教网—

16．

已知椭圆：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的左右焦点分别为F₁（-1，0），F₂（1，0），且过点$（-1，\frac{3}{2}）$，右顶点为A，经过点F₂的动直线l与椭圆交于B，C两点．
（1）求椭圆方程；
（2）记△AOB和△AOC的面积分别为S₁和S₂，求|S₁-S₂|的最大值；
（3）在x轴上是否存在一点T，使得点B关于x轴的对称点落在直线TC上？若存在，则求出T点坐标；若不存在，请说明理由．

分析（1）利用焦点为F（1，0），且过点（-1，$\frac{3}{2}$），列出方程，然后求解椭圆方程；
（2）设直线l方程为：x=my+1．与椭圆联立，设B（x₁，y₁），C（x₂，y₂），（y₁＞0，y₂＜0），利用韦达定理，通过当m=0时，显然|S₁-S₂|=0；当m≠0时，|S₁-S₂|=|$\frac{1}{2}$•2•y₁-$\frac{1}{2}$•2•（-y₂）|=|y₁+y₂|，求解|S₁-S₂|的最大值；
（3）假设在x轴上存在一点T（t，0）满足已知条件，利用k_TB=-k_TC，求出t﹒说明存在点T（4，0）满足条件．

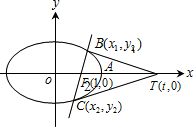解答解：（1）由已知c=1，$\frac{1}{{a}^{2}}$+$\frac{9}{4{b}^{2}}$=1，
又a²-b²=1，
解得a=2，b=$\sqrt{3}$，
即有椭圆方程为：$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1；
（2）设直线l方程为：x=my+1，
联立椭圆方程得（3m²+4）y²+6my-9=0，
设B（x₁，y₁），C（x₂，y₂），（y₁＞0，y₂＜0），
则y₁+y₂=-$\frac{6m}{4+3{m}^{2}}$，
当m=0时，显然|S₁-S₂|=0；
当m≠0时，|S₁-S₂|=|$\frac{1}{2}$•2•y₁-$\frac{1}{2}$•2•（-y₂）|
=|y₁+y₂|=$\frac{6|m|}{4+3{m}^{2}}$=$\frac{6}{3|m|+\frac{4}{|m|}}$≤$\frac{6}{2\sqrt{3•4}}$=$\frac{\sqrt{3}}{2}$，
当且仅当3|m|=$\frac{4}{|m|}$，即m=±$\frac{2\sqrt{3}}{3}$时取等号，
综合得m=±$\frac{2\sqrt{3}}{3}$时时，|S₁-S₂|的最大值为$\frac{\sqrt{3}}{2}$；
（3）假设在x轴上存在一点T（t，0）满足已知条件，
则k_TB=-k_TC
即$\frac{{y}_{1}}{{x}_{1}-t}$=-$\frac{{y}_{2}}{{x}_{2}-t}$，即为y₁（x₂-t）+y₂（x₁-t）=0，
⇒y₁（my₂+1-t）+y₂（my₁+1-t）=0⇒2my₁y₂+（1-t）（y₁+y₂）=0，
即有2m•$\frac{-9}{4+3{m}^{2}}$+（1-t）•$\frac{-6m}{4+3{m}^{2}}$=0，
整理得：（4-t）•m=0，
由m任意，即有t=4﹒
故存在点T（4，0）满足条件﹒

点评本题考查直线与椭圆的位置关系的综合应用，椭圆方程的求法，存在性问题的处理方法，韦达定理以及基本不等式的应用，考查计算能力．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案