解:(I)g′(x)=3x
2+2ax-1由题意3x
2+2ax-1<0的解集是
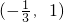
即3x
2+2ax-1=0的两根分别是

.
将x=1或

代入方程3x
2+2ax-1=0得a=-1.
∴g(x)=x
3-x
2-x+2.(4分)
(II)由(Ⅰ)知:g′(x)=3x
2-2x-1,∴g′(-1)=4,
∴点p(-1,1)处的切线斜率k=g′(-1)=4,
∴函数y=g(x)的图象在点p(-1,1)处的切线方程为:
y-1=4(x+1),即4x-y+5=0.(8分)
(III)∵2f(x)≤g′(x)+2
即:2xlnx≤3x
2+2ax+1对x∈(0,+∞)上恒成立
可得
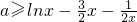
对x∈(0,+∞)上恒成立
设
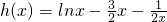
,则
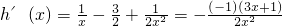
令h′(x)=0,得

(舍)
当0<x<1时,h′(x)>0;当x>1时,h′(x)<0
∴当x=1时,h(x)取得最大值-2
∴a≥-2.
∴a的取值范围是[-2,+∞).(13分)
分析:(I)求出g(x)的导函数,令导函数小于0得到不等式的解集,得到相应方程的两个根,将根代入,求出a的值.
(II)求出g(x)的导数在x=-1的值即曲线的切线斜率,利用点斜式求出切线的方程.
(III)求出不等式,分离出参数A,构造函数h(x),利用导数求出h(x)的最大值,令a大于等于最大值,求出a的范围.
点评:解决不等式恒成立问题,常用的方法是分离出参数,构造新函数,求出新函数的最值,得到参数的范围.

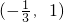 ,求函数g(x)的解析式;
,求函数g(x)的解析式;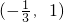
 .
. 代入方程3x2+2ax-1=0得a=-1.
代入方程3x2+2ax-1=0得a=-1.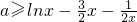 对x∈(0,+∞)上恒成立
对x∈(0,+∞)上恒成立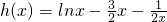 ,则
,则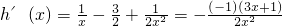
 (舍)
(舍)

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案